b^2/a^3.
Объяснение:
Воспользуемся следующим свойством:
(а/b)^(-n) = (b/a)^n, в нашем случае получим:
(a^3 /b^2)^ (-1) = (b^2/a^3)^1 = b^2/a^3.
x км/ч скорость велосипедиста
х+25 км/ч скорость автомобилиста
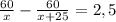
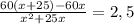
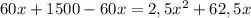
2,5x²+62,5x-1500=0 разделим на 2,5
х²+25х-600=0
D=625+2400=3025
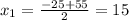км/ч скорость велосипедиста
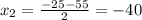не удовлетворяет условию задачи
....................................................................................................................................................................................................................................................................................................................................................
Формула объема призмы: Площадь основания (Sосн.) умножить на высоту (h), тобишь:
Vпризмы=Sосн.*h
Площадь основания правильного шестиугольника равна: три корня из трех на два умножить на сторону в квадрате(a), тобишь:
Sосн.=3√3/2*a^2
Из текста задачи ясно, что объем не изменился. Получаем: V1=V2, а сторона основания второй призмы в два раза меньше, и обозначив сторону первой за a, сторону второй обозначим через a/2.
Приравниванием формулы объема первой и второй призмы,обозначаем искомую высоту через x и получаем уравнение:
3√3/2*a^2*24=3√3/2*a^2/4*x
Делим обе части уравнения на 3√3/2 и получаем:
a^2*24=a^2/4*x
Чтобы избавится от знаменателя во второй части домнажаем обе части на 4:
96*a^2=a^2x
x=96a^2/a^2
В результате a^2 сокращается и остается 96:
x=96.
ответ:96 см.
ответ:
При этом нужно знать, что a⁻ᵇ (где b - натуральное) равно 1/(aᵇ) .