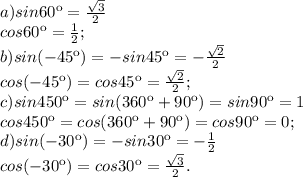
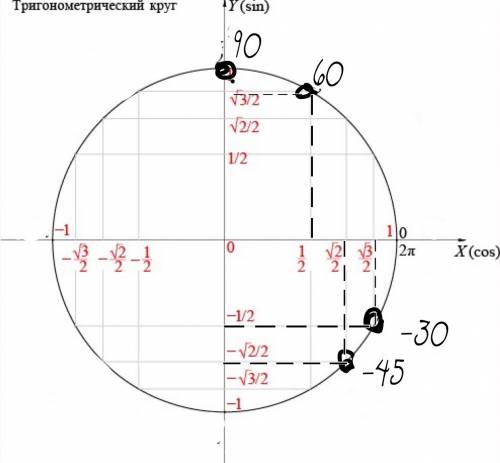
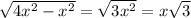, тогда sin60=√3x/2x=√3/2.
.
.
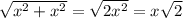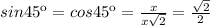В решении.
Объяснение:
Дана функция у=√х:
а) График которой проходит через точку с координатами А(а; 3√3). Найдите значение а.
Нужно в уравнение подставить известные значения х и у (координаты точки А):
3√3 = √а
(3√3)² = (√а)²
9*3 = а
а=27;
b) Если х∈[9; 25], то какие значения будет принимать данная функция?
у= √х
у=√9=3;
у=√25=5;
При х∈ [9; 25] у∈ [3; 5].
с) y∈ [14; 23]. Найдите значение аргумента.
14 = √х
(14)² = (√х)²
х=196;
23 = √х
(23)² = (√х)²
х=529;
При х∈ [196; 529] y∈ [14; 23].
d) Найдите при каких х выполняется неравенство у ≤ 4.
√х <= 4
(√х)² <= (4)²
х <= 16;
Неравенство у ≤ 4 выполняется при х <= 16.
((x+3)(x+3) -x(x -3)) /(x-3)(x+3) =(x² +6x+9 -x² +3x) /(x-3)(x+3) =(9x +9) /(x-3)(x+3) =9(x+1) /(x-3)(x+3)
при делении дробь переворачиваем и будет умножение
9(x +1)*(x+3) /(x-3)(x+3)*(x+1) =9/(x-3)
ответ: 9/(x-3)