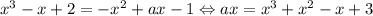
Так как x = 0 не является корнем уравнения, поделим обе части на x.
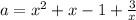
Обозначим правую часть как f(x). Найдём производную этой функции:
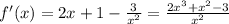
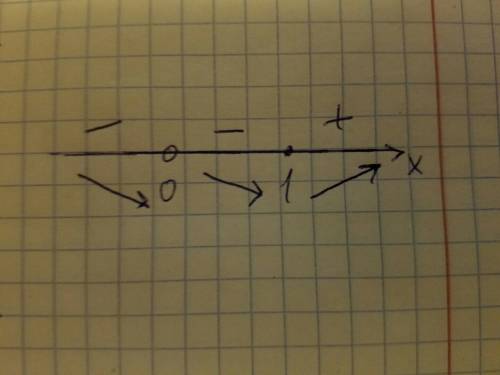
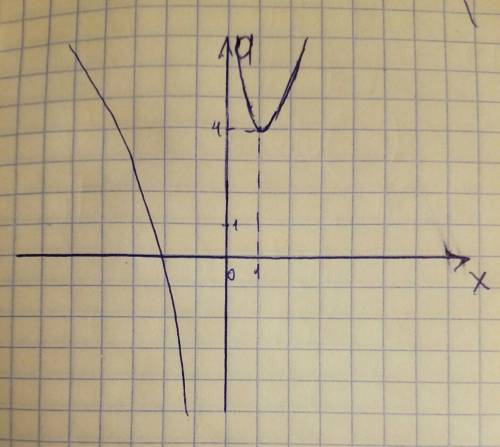
Заметим, что при x = 1 числитель равен нулю. Разложим его на множители: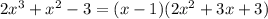 
. Второй множитель разложить нельзя, так как, приравняв его к нулю, мы не сможем найти корни, ибо D < 0. Найдём знаки производной (см. фото 1). Зная это, можем прикинуть график функции (см. фото 2). Точка локального минимума - x = 1. f(1) = 4.
a = k (k - какое-то число) - прямая, параллельная оси Ox. По графику видно, что при a < 4 имеется ровно одно пересечение, то есть один корень.
ответ: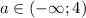 
V(t) = S'(t) = -12t + 6t².
А) Подставляем t = 3 в полученное уравнение.V(3) = -12 × 3 + 6 × 3² = -36 + 6 × 9 = -36 + 54 = 18.
Б) Подставим V = 0 в уравнение зависимости скорости.-12t + 6t² = 0;
6t × (t- 2) = 0;
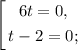
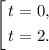
Таким образом скорость будет равна нулю в момент времени: t = 0 и t = 2.
В) Подставим V = 18 в уравнение зависимости скорости.По сути этот пункт можно не решать, ведь он уже решён в А. Но давайте всё же рассмотрим и его.
-12t + 6t² = 18;
6t² - 12t - 18 = 0;
t² - 2t - 3 = 0;
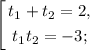
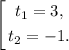
Так как время отрицательным быть не может, t₂ - посторонний корень.
Значит, искомое время 3.
ответ: 18; 0 и 2; 3.
у²-3у - 1 = у² - 2 *1,5 у + (1,5)² - 3,25= (у-1,5)²- 3,25
если у² -3у -1 = 11 , следовательно :
(у-1,5)² - 3,25=11
(у-1,5)²= 11+3,25
(у-1,5)²=14,25
Теперь выделим неполный квадрат из второго выражения:
8у²- 24у - 9 = 8 (у²- 3у - 9/8 ) = 8(у²-3у -1,125) =
= 8 ( у² -3у + 2,25 - 3,375) = 8 (( у-1,5)² - 3,375 ) =
= 8(у-1,5)² - 8 * 3,375 = 8(у-1,5)² - 27
если (у-1,5)²=14,25 , то из второго выражения получается:
8*14,25 -27 = 114-27 = 87
ответ: если у²-3у-1=11 , то 8у²-24у -9 = 87.