Пусть х кг - масса первого сплава, тогда
(215-х) кг - масса второго сплава.
10% от х = 0,1х (кг) - масса свинца в первом сплаве;
35% от (215-х) = 0,35(215-х)= (75,25-0,35х) (кг) - масса свинца во втором сплаве.
215 кг - масса общего сплава,
25% от 215 кг = 0,25 · 215 = 53,75 (кг) - масса свинца в общем (третьем) сплаве;
Получаем уравнение:
0,1х + (75,25-0,35х) = 53,75
0,1х + 75,25-0,35х = 53,75
0,1х - 0,35х = 53,75 - 75,25
- 0,25х = - 21,5
х = - 21,5 : (- 0,25)
х = 86
Если 86 кг - масса первого сплава, тогда
215 - 86 = 129 кг - масса второго сплава.
129 - 86 = 43 (кг)
ответ: на 43 килограмма масса первого сплава меньше массы второго.
Відповідь:
60 МОЖЛИВИХ РОЗМІЩЕНЬ!
Роз'яснення:
1) Всього непарних чисел є п'ять: 1, 3, 5, 7, 9. Питається: скільки трицифрових чисел можна скласти із цих 5 непарних чисел? При цьому числа повинні не повторюватись. Останнє означає, що числа, до прикладу, 555, 551, 551, 115, 177, 133 і т.д. - неможливі, адже в них повторюються 5, 1, 7 і 3 два чи більше разів! До речі, якщо треба скласти трицифрові числа із 5 непарних, тоді і самі трицифрові числа будуть непарними, адже парних немає!
2) Означення розміщення таке: "Кожна впорядкована підмножина, яка містить k елементів даної множини з n елементів, називається розміщенням (accommodation) із n по k елементів. Таким чином, два різних розміщення із даних n елементів по k відрізняються один від одного або складом елементів, або порядком їх розміщення." Такі комбінації чисел нам підходять!
Всього n елементів в нас 5 - це непарні числа; а k елементів, які ми хочемо скласти із 5 непарних чисел, тобто з n, є 3; для прикладу візьмемо довільні два числа, нехай це будуть 135 і 153. - 135 відрізняється від 153 лише порядком розміщення, ми "перетасували" десятки і одиниці. Чи можемо ми вважати такі числа розміщенням із n елементів, тобто з п'яти непарних чисел, по k елементів, тобто із будь-яких трьох чисел, складених із n непарних чисел? - Так, виходячи з означення. Ба більше, числа 135 і 137 - це також одні із сполук розміщення, і вони також будуть враховуватися (виходячи з означення, адже вони відрізняються складом елементів).
Тобто нас просять знайти всі такі трицифрові числа, в яких будуть, по-перше, лише непарні числа (їх 5); по-друге, числа (непарні), які не повторюються (111 чи 117 - не підходять!); і по-третє, числа, склад елементів яких різний (153 чи 159 - "Всьо пучком"). АЛЕ ВСІ ЦІ ЦИФРИ ПОВИННІ БУТИ НЕПАРНИМИ! (їх п'ять, до речі)
3) Таку махінацію можна було б проробити на листочку, що я Вам і рекомендую, щоб переконатися, що формула не бреше. Але ми нею і скористаємося, а для підтвердження її правильності, я додам малюнок із цими розміщеннями.
4) Отож, число розміщень із n елементів по k позначається символом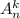 
(arrangement (франц.) - розміщення). Число всіх можливих розміщень із n елементів по k дорівнює добутку k послідовних чисел, з яких найбільшим є n, тобто: 
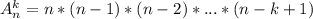(1). Цією формулою варто користуватися при числових розрахункам, що нам і підійде, але зазвичай просять запам'ятати іншу. Виведемо її, поділивши нашу 1 формулу на 
маємо:
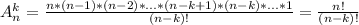(2).
5) Скористаємося першою формулою, пам'ятаючи, що n = 5 (усі непарні числа), а m = 3 (непарні трицифрові числа із 5 непарних):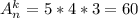 
. Тобто всього чисел, які складені з 5 непарних чисел 1, 3, 5, 7, 9, але водночас які є трицифровими - рівно 60.
