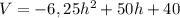
Графиком функции является парабола . Найдём координаты её вершины.
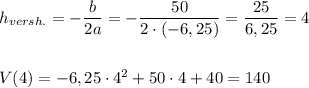
При увеличении глубины погружения до 4 м скорость течения увеличивается. Затем на глубине 4 м она достигает своего max значения. А затем глубина погружения увеличивается ( приблизительно до 9 м ), а скорость течения уменьшается . Смотри график .
При глубине h=4 м скорость течения реки наибольшая и равна V=140 м/мин.
P.S. Река с очень быстрым течением, V=140 м/мин=8,4 км/час ...Наверное, в условии коэффициент перед х² не -6,25 , а -62,5 . Тогда получится, что V=50 м/мин=3 км/час и h=0,4 м . Это более реально .
1) Найдём производную:
2. Найдём экстремумы:
Заданной области принадлежит точка
3. Найдём область убываения и возрастания относительно нуля: с метода интервалов установим, функция убывает на промежутке
4. Найдём вторую производную и исследуем функцию на выпуклость:
Нам повезло — экстремум второй производной лежит вне нашей области. Методом интервалов установим, что функция на области
5. Теперь можно строить график. Найдём значение функции в точках −1 и 1:
6. Суммируя все предыдущие пункты, наносим такие точки:
И теперь соединяем их так, чтобы функция убывала на [-1; 0] и росла— на [0; 1]. И не забываем, что функция везде должна быть вогнута.
Если правильно построишь, должно получиться так: