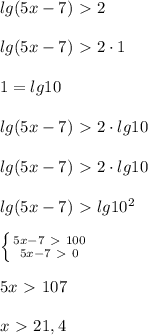
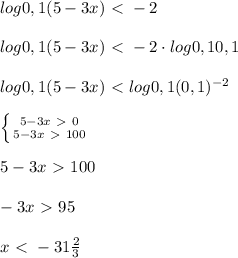
Формулы Виета — формулы, связывающие коэффициенты многочлена и его корни.
Этими формулами удобно пользоваться для проверки правильности нахождения корней многочлена, а также для составления многочлена по заданным корням.
Эти тождества неявно присутствуют в работах Франсуа Виета. Однако Виет рассматривал только положительные вещественные корни, поэтому у него не было возможности записать эти формулы в общем виде.[1]:138—139
Если {\displaystyle c_{1},c_{2},\ldots ,c_{n}} — корни многочлена
{\displaystyle x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots +a_{n}}
(каждый корень взят соответствующее его кратности число раз), то коэффициенты {\displaystyle a_{1},\ldots ,a_{n}} выражаются в виде симметрических многочленов от корней[2], а именно:
{\textstyle {\begin{aligned}a_{1}&=-(c_{1}+c_{2}+\ldots +c_{n}),\\a_{2}&=c_{1}c_{2}+c_{1}c_{3}+\ldots +c_{1}c_{n}+c_{2}c_{3}+\ldots +c_{n-1}c_{n},\\a_{3}&=-(c_{1}c_{2}c_{3}+c_{1}c_{2}c_{4}+\ldots +c_{n-2}c_{n-1}c_{n}),\\&~~\vdots \\a_{n-1}&=(-1)^{n-1}(c_{1}c_{2}\ldots c_{n-1}+c_{1}c_{2}\ldots c_{n-2}c_{n}+\ldots +c_{2}c_{3}...c_{n}),\\a_{n}&=(-1)^{n}c_{1}c_{2}\ldots c_{n}.\end{aligned}}}
Иначе говоря, {\displaystyle (-1)^{k}a_{k}} равно сумме всех возможных произведений из {\displaystyle k} корней.
Следствие: из последней формулы Виета следует, что если корни многочлена целочисленные, то они являются делителями его свободного члена, который также целочисленный.
Если старший коэффициент многочлена не равен единице:
то для применения формулы Виета необходимо предварительно разделить все коэффициенты на {\displaystyle a_{0}} (это не влияет на значения корней многочлена). В этом случае формулы Виета дают выражение для отношений всех коэффициентов к старшему:
{\displaystyle {\frac {a_{k}}{a_{0}}}=(-1)^{k}\sum _{1\leqslant i_{1}<i_{2}<\cdots <i_{k}\leqslant n}c_{i_{1}}c_{i_{2}}\dots c_{i_{k}},\quad k=1,2,\dots ,n.}
Доказательство осуществляется рассмотрением равенства, полученного разложением многочлена по корням, учитывая, что {\displaystyle a_{0}=1}
{\displaystyle x^{n}+a_{1}x^{n-1}+a_{2}x^{n-2}+\ldots +a_{n}=(x-c_{1})(x-c_{2})\cdots (x-c_{n}).}
Приравнивая коэффициенты при одинаковых степенях {\displaystyle x} (теорема единственности), получаем формулы Виета.
Винберг Э. Б. Алгебра многочленов. Учебное пособие для студентов-заочников III—IV курсов физико-математических факультетов педагогических институтов. — М.: Просвещение, 1980.Weisstein, Eric W. Vieta's Formulas / From MathWorld--A Wolfram Web Resource (англ.)Hazewinkel, Michiel, ed. (2001), "Viète theorem" (недоступная ссылка), Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4 (англ.)Funkhouser, H. Gray (1930), "A short account of the history of symmetric functions of roots of equations", American Mathematical Monthly (Mathematical Association of America) 37 (7): 357–365, doi:10.2307/2299273, JSTOR 2299273 (англ.)