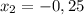1) x^2 - 11 x + 30
Чтобы найти корни решу соответствующее кв.уравнение:
x^2 - 11 x + 30=0
по тиореме обратной тиореме Виета
х₁+х₂=11
=30
отсюда х₁=5
х₂=6
ответ. 5;6.
2) x^2-21x+110
Чтобы найти корни решу соответствующее кв.уравнение:
x^2-21x+110=0
по тиореме обратной тиореме Виета
х₁+х₂=21
х₁*х₂=110
отсюда х₁=10
х₂=11
ответ. 10;11.
3) 4x^2-64
Чтобы найти корни решу соответствующее кв.уравнение:
4x^2-64=0
4х²=64
х²=16
х=±4
ответ. ±4
4)4x^2-2x-0,75
Чтобы найти корни решу соответствующее кв.уравнение:
4x^2-2x-0,75=0
D=b²-4ac=(-2)²+4*4*0,75=4+12=16
х₁=-b-√D/2a=2-4/8=-¼
х²=-b+√D/2a=2+4/8=¾
ответ. -0,25; 0,75
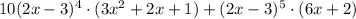
Объяснение:
Для начала необходимо понять, что данное выражение представляет собой произведение двух функций, а для производной от произведения функций существует правило:
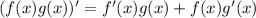
В данном случае 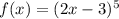 , а
, а 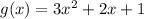
Итак, нам потребуется производная от функции 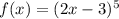 , которая является сложной функцией, производная от которой берется по следующему правилу:
, которая является сложной функцией, производная от которой берется по следующему правилу:

Здесь 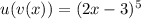 ,
, 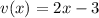
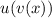 - степенная функция, для нее правило такое:
- степенная функция, для нее правило такое:
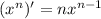
Вычисляем:
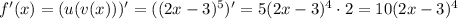
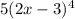 мы получили, когда брали производную от внешней степенной функции , двойка появилась в результате взятия производной от
мы получили, когда брали производную от внешней степенной функции , двойка появилась в результате взятия производной от 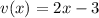 . Т.е.
. Т.е. 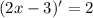
---
Теперь возьмем производную от второго сомножителя в исходном выражении:
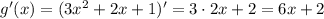
Подставляем все в формулу: ![\[(f(x)g(x))' = f'(x)g(x) + f(x)g'(x)\]](/tpl/images/1008/0917/ca526.png)
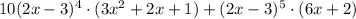
Объяснение:
Найдем производную и приравняем к 0.
g'(x) = 13*3x^2 + 2(a+2)x + (a^2+4a-12) = 0
D/4 = (a+2)^2 - 39(a^2+4a-12) = a^2+4a+4-39a^2-156a+468
D/4 = -38a^2 - 152a + 472 > 0
38a^2 + 152a - 472 < 0
19a^2 + 76a - 236 < 0
D/4 = 38^2 + 19*236 = 5928
a1 = (-38 - √5928)/19 ≈ -6,05
a2 = (-38 + √5928)/19 ≈ 2,05
Нам нужно, чтобы было x1 >= -2; x2 <= 9
x1 = [-a-2 - √(-38a^2-152a+472)]/39 >= -2
x2 = [-a-2 + √(-38a^2-152a+472)]/39 <= 9
Осталось решить эти два неравенства, с учётом области определения
а € ((-38-√5928)/19; (-38+√5928)/19)
Для того чтобы найти корни необходимо данные выражения приравнять к нулю
1)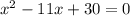
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: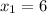 ;
; 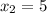
=================================================================
2)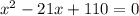
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: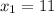 ;
; 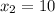
==================================================================
3)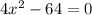
ответ: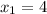 ;
; 
=================================================================
4)
Cчитаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
ответ: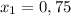 ;
;