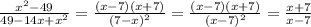
В решении.
Объяснение:
1)Решить неравенство:
(х-4)(х+5)<=0
Раскрыть скобки и решить как квадратное уравнение:
х²+5х-4х-20=0
х²+х-20=0, квадратное уравнение, ищем корни:
D=b²-4ac = 1+80=81 √D=9
х₁=(-b-√D)/2a
х₁=(-1-9)/2
х₁= -10/2
х₁= -5
х₂=(-b+√D)/2a
х₂=(-1+9)/2
х₂=8/2
х₂=4
Теперь начертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -5 и х=4, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у<=0 при х от -5 до 4, то есть, решения неравенства находятся в интервале х∈ [-5, 4], причём значения х= -5 и х=4 входят в решения неравенства.
Неравенство нестрогое, скобки квадратные.
2)х²-х-56>0
Схема решения та же.
Находим корни уравнения:
х²-х-56=0
D=b²-4ac = 1+224=225 √D= 15
х₁=(-b-√D)/2a
х₁=(1-15)/2
х₁= -14/2
х₁= -7
х₂=(-b+√D)/2a
х₂=(1+15)/2
х₂=16/2
х₂=8
Также чертим СХЕМУ параболы (ничего вычислять не нужно), которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -7 и х=8, отмечаем эти точки схематично, смотрим на график.
По графику ясно видно, что у>0 (как в неравенстве), слева и справа от значений х, то есть, решения неравенства в интервалах
х∈ (-∞, -7)∪(8, +∞).
Неравенство строгое, скобки круглые.
3)Решить систему неравенств:
х²-9<=0
2x-5<0
Первое неравенство решим как квадратное уравнение:
х²=9
х₁,₂= ±√9
х₁,₂= ±3
Снова чертим СХЕМУ параболы, которую выражает данное уравнение, ветви направлены вверх, парабола пересекает ось Ох при х= -3 и х=3, отмечаем эти точки схематично, смотрим на график.
По графику видно, что у<=0 при х от -3 до 3, включая эти значения.
Решение неравенства х∈ [-3, 3].
Неравенство нестрогое, скобки квадратные.
Второе неравенство:
2x-5<0
2x<5
x<2,5
Решение неравенства х∈ (-∞, 2,5)
Неравенство строгое, скобки круглые.
Теперь нужно на числовой оси отметить интервалы решений двух неравенств и найти пересечение решений, то есть, такое решение, которое подходит двум неравенствам.
Чертим числовую ось, отмечаем значения -3, 2,5, 3.
Штриховка по первому неравенству от -3 вправо до 3, от 3 влево до -3.
По второму неравенству штриховка от 2,5 влево до - бесконечности.
Пересечение х∈ [-3, 2,5), это и есть решение системы неравенств.
4)Найти наибольшее целое число из решений неравенства:
(х+5)(х-6)² <0
Первое неравенство:
х+5<0
x< -5
Решение неравенства х∈ (-∞, -5);
Во втором неравенстве свёрнут квадрат разности, развернуть, приравнять к нулю и решить как квадратное уравнение:
х²-12х+36=0
D=b²-4ac = 144-144=0 √D= 0
х₁=(-b-√D)/2a
х₁=(12-0)/2
х₁=6
х₂=(-b+√D)/2a
х₂=(12+0)/2
х₂=6
В уравнении один корень, значит, парабола не пересекает ось Ох, а как бы "стоит " на оси Ох, а х=6 это абсцисса (значение х) вершины параболы.
То есть, вся парабола находится выше оси Ох, и не существует значений х, при котором у<0 (как в неравенстве).
Значит, решением данного неравенства будет интервал х∈ (-∞, -5).
Неравенство строгое, х= -5 не входит в число решений, значит, наибольшим целым числом из решений неравенства будет х= -4.
0,5
Объяснение:
Упростить и вычислить: при х= -4
2/(х²-4)+1/(2х-х²) : 1/(х²+4х+4)=
В первых скобках разность квадратов, развернуть, во вторых скобках вынести за скобку х, в третьих скобках квадрат суммы, свернуть:
2/[(х-2)(х+2)] + 1/[x(2-x)] : [1/(x+2)²]=
= в знаменателе второй дроби поменять местами 2 и х: (2-х)= -(х-2), тогда знак плюс перед второй дробью поменяется на минус:
=2/[(х-2)(х+2)] - 1/[x(х-2)] : [1/(x+2)²];
1)Вычитание:
2/[(х-2)(х+2)] - 1/[x(х-2)]=
общий знаменатель х(х-2)(х+2):
=[2*х -1*(х+2)] / [х(х-2)(х+2)]=
=(2x-x-2)/[х(х-2)(х+2)]=
=(x-2)/[х(х-2)(х+2)]=
сокращение (x-2) и (x-2) на (x-2):
=1/[х(х+2)];
2)Деление:
1/[х(х+2)] : [1/(x+2)²]=
=1/[х(х+2)] : [1/(x+2)(х+2)]=
Чтобы разделить дробь на дробь, нужно числитель первой дроби умножить на знаменатель второй дроби, а знаменатель первой умножить на числитель второй дроби:
=[1*(x+2)(х+2)] / [х(х+2)*1]=
=[(x+2)(х+2)] / [х(х+2)]=
сокращение (x+2) и (х+2) на (х+2):
=(х+2)/х=
=(-4+2)/-4=
= -2/-4=0,5.