Задание 83(2)
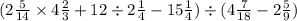
Сначала переведем все правильные дроби в неправильные. Для этого, если, например, дробь

то нужно 14 умножить на 2 и добавить 5(такое правило действует для всех дробей): 14×2+5= 28+5= 33. Знаменатель остаётся 14.
Таким образом,
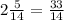
Итак, перепишем пример с условие, только дроби уже все будут неправильными) Получаем вот такое:
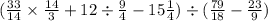
Рассмотрим умножение

Чтобы умножить, нужно сократить те числа, которые можно, ну и поделить. То есть 33:3= 11, 14 и 14 сокращаются. И вот как мы это делаем:

Рассмотрим деление
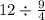
Деление нужно сделать умножением, а для этого в делителе нужно поменять знаменатель и числитель местами. Получаем:
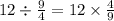
Умножаем:
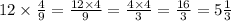
Теперь перепишем пример, уже вставляя готовые решения умножения и деления:
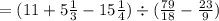
Решим пример

Для начала нужно найти общий знаменатель. 18 и 9...
Мы знаем, что 9×2=18. Тогда общий знаменатель- 18 и дробь которую мы отнимаем, нужно сделать со знаменателем 9(то есть ее нужно умножить на 2, потому что 9×2=18), первую дробь не трогаем.
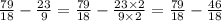
И просто отнимаем 79-46= 33. Знаменатель 18 остаётся.

Получаем это:
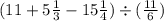
А это в свою очередь равно:
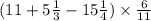
Решим часть примера
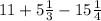
Сначала решим это:

Теперь отнимаем ту дробь.
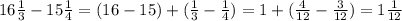
Осталось умножить...
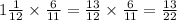
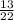
Очень надеюсь, что я тебе Если непонятно какое-то из действий, обращайся. Всегда рада удачи!
-25=6-5x
5x=-31
X=31/5