Question

Вычислить несобственные интегралы или установить их расходимость

Answer 1

$\int\limits^{\infty }_{e}\, \frac{dx}{x\cdot (lnx)^3}=\lim\limits _{A \to +\infty}\int\limits^{A}_{e}\, \frac{\frac{dx}{x}}{(lnx)^3}=\lim\limits _{A \to +\infty}\int\limits^{A}_{e}\frac{d(lnx)}{(lnx)^3}=\lim\limits _{A \to +\infty}\Big (\frac{(lnx)^{-2}}{-2}\Big |_{e}^{A}\Big )=\\\\\\=\lim\limits _{A \to +\infty}\Big (-\frac{1}{2\cdot (lnx)^2}\Big |_{e}^{A}\Big )=\lim\limits _{A \to +\infty}\Big (-\frac{1}{2(lnA)^2}+\frac{1}{2(lne)^2}\Big )=\\\\\\=\Big [\; lnA\to +\infty \; ,\; (lnA)^2\to +\infty \; ,\; \; \frac{1}{(lnA)^2}\to 0\; \; ;\; \; lne=1\; \Big ]=-0+\frac{1}{2}=\frac{1}{2}$

Answer 2

Объяснение:

$\int\limits^x_e {\frac{1}{x(ln(x))^3} } \, dx = \int\limits^x_e {\frac{1}{(ln(x))^3} \, d(ln(x)) = \int\limits^x_e {ln^{-3}(x)} \, d(ln(x)) = \frac{ln^{-2}(x)}{-2} = -\frac{1}{2} * \frac{1}{ln^{2}(x)}$

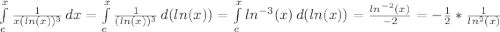
Подставляя верхние и нижние пределы, получим:

$-\frac{1}{2} ( \frac{1}{ln^2(x)} - \frac{1}{ln^2e}) = -\frac{1}{2} ( \frac{1}{ln^2(x)} - 1)$

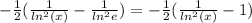
При устремлении x→∞ ln²(x) → ∞, а 1/(ln²(x)) → 0.

Следовательно, данный несобственный интеграл сходится к 1/2.