В озере течения нет, значит по озеру катер S₁=20t₁ .
По реке катер шёл против течения, т.к. катер находился сначала в озере, а потом шёл вверх по реке. Значит S₂=(20-2)t₂=18t₂
Известно, что S₁=S₂, а так же что t₁+t₂>1.9, то есть
20t₁ = 18t₂ ⇒ 10t₁ = 9t₂
Если мы возьмём t₁ = 0.9, а t₂ = 1, то равенство сработает, но сумма будет равна 1,9 часа, что противоречит условию, так как известно, что катер шёл больше 1,9 часа. Значит нужно взять и умножить оба времени на 1,1 к примеру. Тогда получится:
t₁ = 0.9*1.1 = 0.99
t₂ = 1*1.1 = 1.1
S₁ = 20 * 0.99 = 19.8
S₂ = 18 * 1.1 = 19.8
S₁ = S₂ - условие удовлетворено
t₁+t₂ = 0.99 + 1.1 = 2.09 > 1.9 - условие удовлетворено
S₁ = S₂ = 19.8 км
S = 2*19.8 = 39.6 км
426.
1)(х-5)(х-6)=30
х²-5х-6х+30=30
х²-11х+30-30=0
х²-11х=0
х(х-11)=0
Произведение равно 0 если хотя бы один из множителей равен 0.
х-11=0 или х=0
х=11
ответ: 0; 11.
2)(х+2)(х+3)=6
х²+2х+3х+6-6=0
х²+5х=0
х(х+5)=0
Произведение равно 0 если хотя бы один из множителей равен 0.
х+5=0 или х=0
х=-5
ответ: -5; 0.
3)(х-1)(х-4)=3х
х²-х+4-4х-3х=0
х²-8х+4=0
а=1, b=-8, c=4
D=(-8)²-4×4=64-16=48
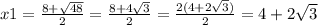
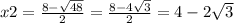

4)(х-2)(х+8)=6х
х²-2х+8х-16=6х
х²+6х-16-6х=0
х²-16=0
х²=16
х=+-4
ответ:-4;4.
427.
1)х²+3х-88=0
а=1, b=3, c=-88
D=3²-4×(-88)=9+352=361
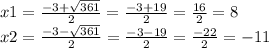
ответ: -11;8.
2)х²+3х-88=20
х²+3х-108=0
а=1, b=3, c=-108
D=3²-4×(-108)=9+432=441
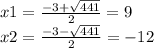
ответ:-12;9.
3)х²+3х-88=-18
х²+3х-70=0
а=1, b=3, c=-70
D=3²-4×(-70)=9+280=289
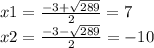
ответ:-10; 7.
4)х²+3х-88=-70
х²+3х-18=0
а=1, b=3, c=-18
D=3²-4×(-18)=9+72=81
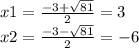
ответ:-6; 3.
428.
1)а=3, b=1, c=-4
D=1²-4×3×(-4)=1+16×3=49>0=>2 корня
2)а=5, b=2, c=3
D=2²-4×5×3=4-60=-56<0=>нет действительных корней
3)а=25, b=-10, c=1
D=(-10)²-4×25=100-100=0=>1 корень
4)а=1, b=0, c=-25
D=0²-4×(-25)=0+100=100>0=>2 корня.
Составим уравнение:
x+2x+2x=20
5x=20
x=20/5
x=4 см(основание треугольника)
2*4=8см(боковые стороны)
ответ:4см,8см,8см