2x^-5x-12/2x+3
Чтобы сократить эту дробь, нужно разложить числитель и знаменатель на множители:
1) 2x^-5x-12 = а(х-х1)(х-х2); а - коэффициент перед х^2
Находим х1 и х2 через дискриминант:
D = b^2 - 4ac = 25 - (-96) = 121; √D = 11
x1 = (-b+√D)/2a = (5+11)/4 = 16/4 = 4
x2 = (-b-√D)/2a =(5-11)/4 = -6/4 = -3/2 = -1,5
Возвращаемся к формуле, подставляем полученные корни:
2x^-5x-12 = 2(х-4)(х+1,5)
2) 2х+3 = 2(х+1,5)
Возвращаемся к дроби, подставляем разложенные числитель и знаменатель:
2(х-4)(х+1,5)/2(х+1,5)
Сокращаем одинаковые множители и получаем ответ: х-4.
Объяснение:
∈ 
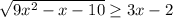
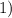
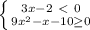
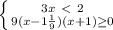
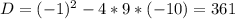
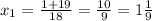
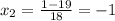
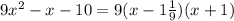
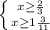
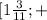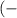∞ ![;-1]](/tpl/images/0674/0179/c47ae.png)
∈ 
∞ 
∈ ∞ ∪ ∞ 
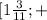= 3с² + 4с + 25