Привет, ты столкнулся с неравенством, буду рада тебе Сначала решаем левую сторону как обычное квадратное уравнение и находим корни) Затем важно определить вид графика (перед нами парабола) Так же, важо узнать в каком направлении направлено ветви графика (в нашем случае параболы) направление ветвей можно определить взглянув на знак, стоящий перед числом с квадратом (Х^2), перед ним стоит знак +, следовательно, ветви параболы направлены вверх. В конце, после решения неравенства нам нужно построить "график" (пример на фото) строим ось Х и на ней отмечаем, приблизительно, корни уравнения. теперь еще одно не менее важное замечание. Если дан знак "больше" или "меньше", то точки на оси будут пыстые (выколотые), как на фото. А если дан знак "больше или равно" или " меньше или равно", то точки на оси будут закрашены. Поставив точки мы должны нанести штриховку (пример на фото) направление штриховку зависит от направления острого конца знака неравенства. затем записываем ответ, в изначальное уравнении стоит знак больше, значит нам нужны участки больше нуля, это от "минус бесконечности" до -5 и от 2 до "плюс бесконечности" ответ записываем таким образом. как на фото. Вид скидок в ответе так же зависит от знака неравенства. На фото ты увидеть небольшую подсказку по этому поводу от меня) P.S. саму параболу рисовать не нужно, но можно, как небольшая подсказка.
Парабола симметричная фигура . это ясно. если сложить ее по оси симметрии, то две ее ветви сольются. то есть сгибать ее надо в точке минимума, так как именно в этой точке она из убывающей становится возрастающей. эта ось симметрии будет параллельна оси оу . осталось найти координаты точки перегиба.(вершины параболы). для этого есть красивая формула . x0 = - b / 2a. y = 2 x^2 - 5 x + 1; a = 2 ; b = - 5; x0 = 5/4 = 1,25. тогда уравнение оси симметрии примет вид х = 1,25. другими словами, при любом значении у значение х будет равно 1,25. это линия - вертикальная ось . перпендикулярно оси 0х через точку х =1,25 проводим линию и получаем ось симметрии.
ответ: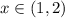
.
Объяснение:
Чтобы долго не решать систему, решим графически . Построим графики
и 
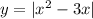. Точки пересечения графиков х=1 и х=2 . График 
лежит ниже графика 
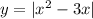при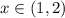 
.