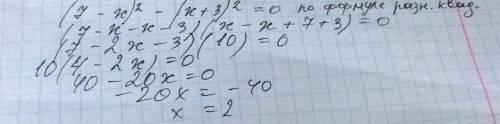
a) x∈ (-∞;3)
b) x∈ (-∞;0] ∪ [4;+∞)
c) x∈ (-∞;0)∪(0;2/3)
d) x∈ [-1/2;1) ∪ (1;+∞)
Объяснение:
a) f(x)=√(-x+3);
-x+3≥0; -x≥-3; x≤3.
ОО: x∈(-∞;3).
b) f(x)=√(0,5x²-2x); 0,5x²-2x≥0; x(0,5x-2)≥0;
x≥0;
0,5x-2≥0; x≥2/0,5; x≥4; x∈[4;+∞);
x≤0;
0,5x-2≤0; x≤2/0,5; x≤4; x∈(-∞;0];
OO: x∈(-∞;0] ∪ [4;+∞);
c) f(x)=ln(2/x-3);
2/x-3>0; 2/x>3; x<2/3; x∈(-∞;2/3);
x≠0; x∈(-∞;0)∪(0;+∞)
OO: x∈(-∞;0)∪(0;+∞) ∩ (-∞;2/3) ⇒ x∈(-∞;0)∪(0;2/3)
d) f(x)=√(3/(x-1)+2);
3/(x-1)+2≥0; 3+2(x-1)≥0; x≥-1/2; x∈[-1/2;+∞)
x-1≠0; x≠1; x∈(-∞;1)∪(1;+∞)
OO: x∈[-1/2;+∞) ∩ (-∞;1)∪(1;+∞) ⇒ x∈[-1/2;1)∪(1;+∞)
Мода - 5
Медиана - 4
Среднее арифметическое - 3,6
Размах - 5
Объяснение:
Мода (число, которое встречается чаще всех), чаще всех встречается число - 5, потому что его тут 3, а остальные по 2 и по 1 разу, значит 5 это мода.
Размах - разность, между наибольшим и наименьшим.
Наибольшее - 6, наименьшее - 1, 6-1=5.
Ср. арифметическое - Сумма всех чисел и делить на их количество.
1+1+2+3+4+4+5+5+5+6 = 36, чисел всего - 10, делим 36 на 10 = 3,6.
Медиана - среднее число (в середине)
1,1,2,3,4,4,5,5,5,6 - тут чётное количество, но в середине стоят две четвёрки, то есть между 4 и 4 стоит 4, поэтому медиана = 4.
49 - 14х + х^2 = х^2 + 6х + 9
6х + 14х = 49 - 9
20х = 40
х = 2