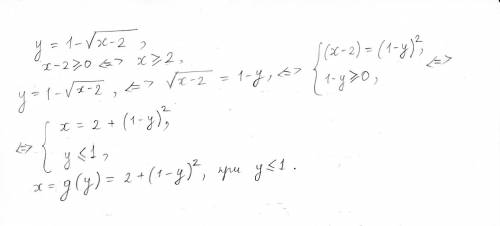
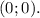
Объяснение:
Данная функция 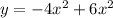 является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
является квадратичной функцией (многочлен второй степени) и задаёт квадратичную параболу. Как известно, у такой функции может быть лишь один экстремум, находящийся в вершине параболы.
Упростим исходную функцию: 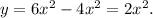
Для нахождения  единственного экстремума воспользуемся производной:
единственного экстремума воспользуемся производной: 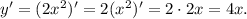
По лемме Ферма, значение производной от  экстремума нулевое. Таким образом,
экстремума нулевое. Таким образом,  точки экстремума будет решением
точки экстремума будет решением 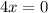 .
.
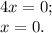
Для нахождения 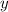 точки экстремума вычислим значение исходной функции от найденного
точки экстремума вычислим значение исходной функции от найденного  :
:
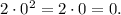
Получается, что координаты точки экстремума это 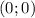 .
.