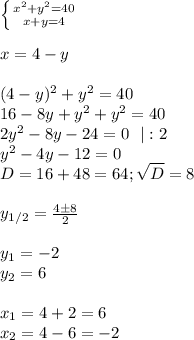
У нас есть правильный многоугольник. Поставим внутрь его точку, и проведем от этой точки отрезки ко всем углам многоугольника.
В итоге многоугольник разделится на треугольники.
Смотрим рисунок, на нем правильный 6-угольник.
Треугольников всегда будет столько же, как углов у многоугольника.
Сумма углов в каждом треугольнике равна 180°.
Сумма уголов во всех n треугольниках равна (180*n)°.
Сумма углов вокруг начальной точки (красная окружность) равна 360°.
Сумма углов многоугольника равна (180*n - 360)° = 180(n - 2)°
Так как многоугольник правильный, то все углы одинаковые.
Каждый угол равен 180(n - 2)/n. По условию он равен 108°.
180(n - 2)/n = 108
180(n - 2) = 108n
180n - 360 = 108n
180n - 108n = 360
n = 360/(180 - 108) = 360/72 = 5
У нас есть правильный многоугольник. Поставим внутрь его точку, и проведем от этой точки отрезки ко всем углам многоугольника.
В итоге многоугольник разделится на треугольники.
Смотрим рисунок, на нем правильный 6-угольник.
Треугольников всегда будет столько же, как углов у многоугольника.
Сумма углов в каждом треугольнике равна 180°.
Сумма уголов во всех n треугольниках равна (180*n)°.
Сумма углов вокруг начальной точки (красная окружность) равна 360°.
Сумма углов многоугольника равна (180*n - 360)° = 180(n - 2)°
Так как многоугольник правильный, то все углы одинаковые.
Каждый угол равен 180(n - 2)/n. По условию он равен 108°.
180(n - 2)/n = 108
180(n - 2) = 108n
180n - 360 = 108n
180n - 108n = 360
n = 360/(180 - 108) = 360/72 = 5
{x+y=4
Во втором уравнении системы выразим Х через У: x=4-y
Подставим x=4-y в первое уравнение вместо Х:
{(4-y)^2+y^2=40
{x=4-y
Решим первое уравнение:
(4-y)^2+y^2=40
16-8y+y^2+y^2-40=0
2y^2-8y-24=0|:2
y^2-4y-12=0
D=(-4)^2-4*1*(-12)=64
y1=(4-8)/2=-2
y2=(4+8)/2=6
Находим значения Х:
1)если у=-2, то x=4-(-2)=6
2) если y=6, то x=4-6=-2
ответ: (6;-2) (-2;6)