6x² - 11x - 2 < 0
Рассмотрим квадратичную функцию у = 6x² - 11x - 2. Графиком этой функции является парабола, ветви которой направлены вверх.
Выясним, как расположена эта парабола относительно оси Ох. Для этого решим уравнение 6x² - 11x - 2 = 0:
D = (-11)² - 4 · 6 · (-2) = 121 + 48 = 169; √169 = 13
х₁ = (11 + 13)/(2 · 6) = 24/12 = 2
х₂ = (11 - 13)/(2 · 6) = -2/12 = -1/6
Значит, парабола пересекает ось Ох в двух точках, абсциссы которых равны -1/6 и 2.
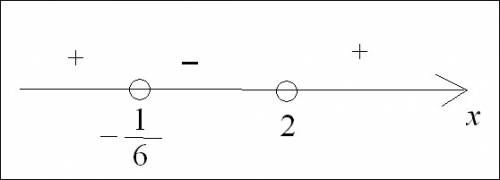
Покажем на чертеже, какие значения (по знаку) принимает функция на каждом из промежутков числовой оси (см. рис. в приложении).
х ∈ (-1/6; 2)ответ: (-1/6; 2).
3^2 +4^2 = 9 + 16 =25
5^2 = 25
25=25
б) 10^2 -6^2 > (10-6)^2
10^2-6^2 = 100-36 = 64
(10-6)^2 = 4^2 = 16
64>16
в) -2^4 < (-2)^4
-2^4 = - 16
(-2)^4 = 2^4 = 16
-16<16
г) (2*3)^2 = 2^2 *3^2
(2*3)^2 = 6^2 = 36
2^2 * 3^2 = 4*9 =36
36=36