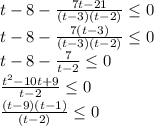
Объяснение:
1) у=6х²
х₀= -b/2a=0
y₀=0
Координаты вершины параболы (0; 0)
2) у=(х-2)²-1
у=х²-4х+4-1
у=х²-4х+3
х₀= -b/2a=4/2=2
y₀=2²-4*2+3=4-8+3= -1
Координаты вершины параболы (2; -1)
3) у= -2(х+4)²
у= -2(х²+8х+16)
у= -2х²-16х-32/2
у= -х²-8х-16
х₀= -b/2a=8/-2= -4
y₀= -(-4)²-8*(-4)-16= -16+32-16=0
Координаты вершины параболы (-4; 0)
4) у=(х-4)²+5
у=х²-8х+16+5
у=х²-8х+21
х₀= -b/2a=8/2=4
y₀=4²-8*4+21=16-32+21=5
Координаты вершины параболы (4; 5)
5) у= х²-2х+4
х₀= -b/2a=2/2=1
y₀=1²-2*1+4=1-2+4=3
Координаты вершины параболы (1; 3)
6) у=2х²-5
х₀= -b/2a=0/2=0
y₀=0-5= -5
Координаты вершины параболы (0; -5)
7) у = -х²+4х
х₀= -b/2a= -4/-2= 2
y₀= - (2)²+4*2= -4+8=4
Координаты вершины параболы (2; 4)
Тогда решение будет следующим:
ОДЗ:
Знаменатель дроби не может быть равен 0. Найдём корни при которых знаменатель будет равняться 0, чтобы потом исключить их из решения
9ˣ-5*3ˣ+6=0 3ˣ-3=0
3²ˣ-5*3ˣ+6=0 3ˣ=3
Вводим замену переменной x=1
3ˣ=t
t²-5t+6=0
D=25-24=1
t=(5-1)/2=2 t=(5+1)/2=3
3ˣ=2 3ˣ=3
x=log₃2 x=1
x≠log₃2 и x≠1
Далее раскрываем скобки в числителе и переносим дробь из правой части неравенства, а также вводим замену переменой
3ˣ=t
Корни знаменателя мы нашли ранее, поэтому работаем с числителем:
(-5t+11)(t-3)=0
-5t²+15t+11t-33=0
-5t²+26t-33=0
D=26²-4*(-5)*(-33)=676-660=16
t=(-26-4)/-10=3 t=(-26+4)/-10=11/5=2,2
3ˣ=3 3ˣ=2,2
x=1 x=log₃2,2