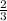 от того, что осталось после первого деня, то после второго дня работы осталась
от того, что осталось после первого деня, то после второго дня работы осталась  от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно
от того, что осталось после первого дня работы. По условию, после двух дней работы осталось 2 банки, соответственно  =2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
=2, из чего следует, что во второй день израсходовали 4 банки с краской (так как 2×2=4). По условию сказано, что в первый день израсходовали половину всех банок +1. Значит, 4 банки - это половина всех банок -1. Соответственно, половина - это 4+1=5. В первый день израсходовали 5+1=6 (банок с краской), во второй день израсходовали 4 (банки с краской), а осталось на третий день еще 2 (банки с краской). Суммируем все количество банок: 6+4+2=12.
2^*x-2)-2/(2^(x-2))=1
2^(x-2)=a
a-2/a-1=0
a²-a-2=0
a1+a2=1 U a1*a2=-2
a1=-1⇒2^(x-2)=-1 нет решения
a2=2⇒2^(x-2)=2⇒x-2=1⇒x=3
2
2=3*4^(1-x)*4^2x
2=12*4^x
4^x=1/6
x=log(4)1/6=-log(4)6