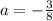
Объяснение:
Здесь стоит использовать небезызвестную теорему Виета. Согласно ей, сумма корней равна второму коэффициенту с противоположным знаком, а их произведение равно свободному члену.
Второй коэффициент: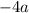 
.
Свободный член: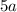 
Стало быть,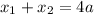 
,
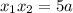
Только вот дело в том, что у нас нет ни суммы, ни произведени корней, а только сумма их квадратов. Выход прост: достаточно вспомнить одну из формул сокращенного умножения:
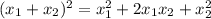
Выражаем отсюда сумму квадратов:
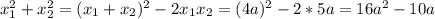
Из условия она равна 6:
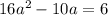
Решаем квадратное уравнение:
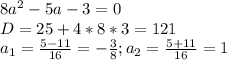
Значения параметра получены, но еще рано писать их в ответ. Дело в том, что теорема Виета никак не может гарантировать, что корни уравнений при каждом из а будут различными: в общем случае они могут и совпадать или их вообще может не быть. От нас же в задаче требуют их наличие и, к тому же, различные. Следовательно, нужно проверить именно это относительно каждого а.
Тактика следующая: подставляем в общее уравнение каждое из а. Имеем два разных квадратных уравнения. За отличие корней, как известно, отвечает условие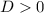 
.
1). 
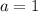
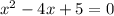
- вообще корни отсутствуют. Значит, данное значение а нас не устраивает.
2). 
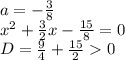- два различных корня.
Таким образом, лишь при 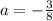в полной мере достигаются все заданные требования. Это и есть ответ.
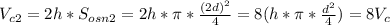
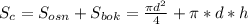
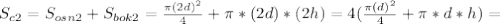
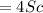
=-2х^2-4х-3