4/7 * (0,56 - 4,2у) + 0,4 = 5/13 * (0,52 - 6,5у)
4/7 * 56/100 - 4/7 * 42/10у + 0,4 = 5/13 * 52/100 - 5/13 * 65/10у
8/25 - 24/10у + 0,4 = 1/5 - 5/2у
- 2,4у + 2,5у = 0,2 - 0,32 - 0,4
0,1у = - 0,52
у = - 0,52 : 0,1
у = - 5,2
Проверка: 4/7 * (0,56 - 4,2 * (- 5,2) + 0,4 = 5/13 * (0,52 - 6,5 * (- 5,2))
4/7 * (0,56 + 21,84) + 0,4 = 5/13 * (0,52 + 33,8)
4/7 * 22,4 + 0,4 = 5/13 * 34,32
4/7 * 224/10 + 0,4 = 5/13 * 3432/100
12,8 + 0,4 = 264/20
13,2 = 13,2
ответ: у = - 5,2.
Простое число р при р>3 имеет вид р=6k+1 или p=6l-1, где k, l - некоторые натуральные числа
Поэтому либо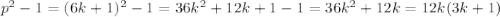 
делится на 12, так как множитель 12 делится на 12, а один из множителей k или 3k+1 делится на 2(если k четное, значит k - делится на 2, если k - нечетное, то 3k+1- четное и делится на 2)
либо
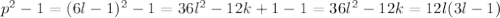делится на 12, так как множитель 12 делится на 12, а один из множителей l или 3l-1 делится на 2(если l четное, значит l - делится на 2, если l - нечетное, то 3l-1- четное и делится на 2)
В обоих возможных случаях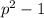 
делится на 12*2=24. Доказано
x^2+y^2=25
3x+4y=z
Вместо z подставляете число из приведённого списка и решаете систему.
Похоже, что будет какое-нибудь бредовое число, не удовлетворяющее равенству.
Например,
x^2+y^2=25
3x+4y=25
x=(25-4y)/3
625-200y+16y^2/9+y^2=25
16y^2-200y+625+9y^2=225
25y^2-200y+400=0
y^2-8y+16=0
D=64-64=0
y=8/2=4
x=(25-4y)/3=3
Если сделать проверку, то убедимся, что 3x+4y может равняться 25.
Думаю, вы поняли принцип.