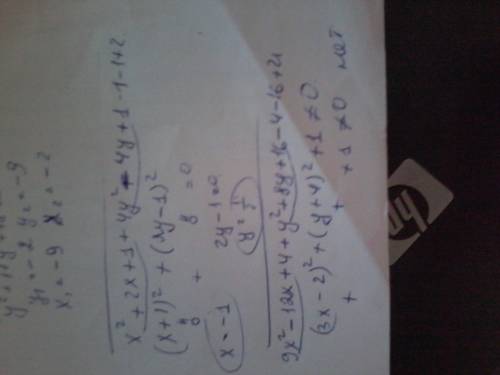
Объяснение:
1) разложим числитель и знаменатель на множители. Из числителя вынесем 8 как общий множитель, в знаменателе воспользуемся формулой сокращённого умножения a^2-b^2 = (a-b)(a+b). Тогда будет 8*(x+4)/((x-4)(x+4)) => 8/(x-4) учитывая что x≠-4
2) 1) 7a/(b-3) и b/((b-3)(b+3)) => 7a*(b+3)/((b-3)(b+3)) и b/((b-3)(b+3))
Под 2) 1/(х-3)^2 и 1/((х-3)(х+3)) => (х+3)/((х-3)^2)*(х+3)) и (х-3)/((х-3)^2)*(х+3))
Номер 3)
1) t^2/(3*(t-2)) + 4/(3*(2-t)) => t^2/(3*(t-2)) — 4/(3*(t-2)) => (t^2-4)/(3*(t-2)) => (t+2)/3 с учётом t≠-2
2) a^2/((a-8)(a+8)) - a/(a+8) => (a^2-a*(a-8))/((a-8)(a+8)) => 8a/((a-8)(a+8))
если скорость велосипедиста в первый день была х, то время, которое он затратил было 98/х
во второй день его скорость была х+7, а время 98/(х+7) и еще 7 часов, что он отдыхал в дороге.
Получается уравнение:
98/х=7+98/(х+7)
поскольку уравнение можно сократить на 7, я это и делаю, чтобы легче решать
14/х=1+14/(х+7)
приводим к общему знаменателю, переносим все в левую часть:
(14х+98-14х-x^2-7x)/(x^2+7x)
х≠0 x≠-7
14х+98-14х-x^2-7x=0
98-x^2-7x=0
Решаем кв. уравнение
√D=21
x1=7
x2=-14 скорость не может быть отрицательной
Проверяем:
98/7=7+98/14
14=14 правда
ответ 7 км/час
=(x+1)²+4*(y-1/2)². Очевидно, что многочлен обращается в 0 при x=-1 и y=1/2.
2) 9*x²+y²-12*x+8*y+21=9*(x²-4*x/3)+(y+4)²-16+21=9*((x-2/3)²-4/9)+(y+4)²+5
=9*(x-2/3)²+(y+4)²+1≥1 при любых значениях x и y. Поэтому таких значений нет.