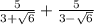
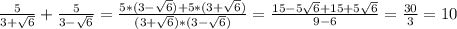
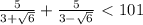
а) y=(x-2) в 4 степени
1)Четная
2)Определена на всей области определения
3)Вершина в точке (2;0)
4)Ветви направлены вверх.
5)До x<2 убывает.
6)При x>4 возрастает.
б)0.5sinx+2
1) Определена на всей области определения
2) Нечетная
3) Периодическая
4) Возрастает и убывает
5) Знакопостоянна на промежутках
6) Непрерывна
7) График называеться синусойдой
в)y=0.5cosx+2
1)Определена на всей области определения
2)Четная
3)Периодическая
4)Область значений отрезок [ 1,5; 2,5];
5)Убывает на промежутках [KeZ; п+2пk] и возрастает на промежутках [п+2пk;KeZ]
Г)y=-(x+2)в 4 степени.
1)Определена на всей области определения
2) Вершина в точке (-2;0)
3)Возростает (-бесконечности;-2);
4)Убывает (-2;+бесконечности);
5)Ветви направлены в низ
6) Область значений (0;-бесконечности)
7) Ость оссимптот: x=-2
8)Наибольшее значение при y=0; x=-2
9) Наименьшего значения не существует
х км/ч- скорость 1 автобуса
(х+4) км/ч- скорость 2 автобуса
S=72 км
72/х час-время 1 автобуса
72/(х+4) час- время 2 автобуса
Один автобус прибыл на 15 минут раньше, т.е на 1/4ч или 0.25часа
72/х-72/(х+4)=0,25- умножим обе части уравнения на х(х+4), при условии,
что х(х+4) не равно нулю.
72х+288-72х=0,25х^2+x
0.25x^2+x-288=0-умножим обе части уравнения 4
x^2+4x-1152=0
D=4^2-4*(-1152)=16+4608=4624
x1=(-4+68)/2=64/2
x1=32
x2=(-4-68)/2=-72/2
x2=-36-корень не является нашим решением уравнения
х км/ч- скорость 1 автобуса=32км/ч
(х+4) км/ч- скорость 2 автобуса=32+4=36км/ч
2,25-2=0,25
0,25=0,25-Один автобус прибыл на 15 минут раньше(0.25часа или 1/4часа)
Итак, надо сравнить данную дробь и корень из 101. Это записывается на языке математики так:
Здесь вот эта закорючка в центре показывает, что вместо неё должен стоять один из знаков(больше или меньше). В конце мы его выставим.
Дальше работаем с этой сравнимостью.
Мы можем запросто перебрасывать слагаемые из одной части в другую, умножать и делить на положительные числа, в общем, представить, что вместо закорючки стоит знак равенства и делать обычные вещи, к которым мы всегда привыкли. Мы сделаем следующее - возведём обе части в квадрат. Делали же мы такое с равенствами? Делали. В уравнениях, например. Здесь это очень хороший шаг, поскольку мы можем этим действием избавиться от корня в правой части. Что получим? Числа. А их мы можем спокойно сравнивать. Делаем это.
Что же у нас всё таки больше? Понятно, что 101. Значит, правая часть будет больше левой. Так что,
Ещё раз, почему мы это сделали? Потому что в последней сравнимости мы поставили знак <(100/9 заведомо меньше, чем 101). А какой знак поставили в последнем выражении, такой и в основном.
Это был наиболее простой случай. В более сложных помимо возведения в квадрат приходится делать что-то ещё. Но цель одна - с корнями нам не хочется работать, так что будем сравнивать те же выражения, но без корней. После того, как мы дойдём до такого выражения, какое у нас в конце получилось, мы с чистой совестью ставим уже понятно какой знак, такой же знак и будет стоять в выражениях с корнями. Как делать всё это, непростой вопрос. Нет приёмов на все случаи жизни, на то она и математика. Если будут вопросы, обращайтесь.