А)(2х+3)² б)(7у-6)² в)(10+8к)² г)(5у-4х)² д)(5а+1/5b)² (1/5) это не разделить а дробь е)(1/4m-2h)² ж)(0,3x-0,5a)² з)(10c+0,1y)² a)(7-8b)² б)(0,6+2x)² в)(1/3x-3y)² г)(4a+1/8b)² д)(0,1m+5n)² е по быстрее)

👇

Ответ:

Sdq2

02.06.2022

А) (2х + 3)² = 4х² + 12х + 9б) (7у -6)² = 49у² - 84у + 36
в) (10 + 8к)² = 100 + 160к + 64к²
г) (5у - 4х)² = 25у² - 40ху + 16х²
д) (5а + 1/5b)² (1/5) = (25a² + 2ab + 1/25b²) * 1/5 = 5a² + 2/5ab + 1/125b²
е) (1/4m - 2h)² = 1/16m - mh + 4h²
ж) (0,3x - 0,5a)² = 0,09x² - 0,3ax + 0,25a²
з) (10c + 0,1y)² = 100c² + 2cy + 0,01y²
a) (7 - 8b)² = 49 - 112b + 64b²
б) (0,6 + 2x)² = 0,36 + 2,4x + 4x²
в) (1/3x - 3y)² = 1/9x² - 2xy + 9y²
г) (4a + 1/8b)² = 16a² + ab + 1/64b²
д) (0,1m + 5n)² = 0,01m² + mn + 25n²
е) (12a - 0,3c)² = 144a - 7,2ac + 0,09c²

4,4(27 оценок)

Открыть все ответы

Ответ:

sodemAN2

02.06.2022

Объяснение:

Подкоренное выражение х²-5х+6 /х-4 ≥0 х²-5х+6 ≥ 0 0 ∠ х-4

(х-3)(х-2)≥0

это точки пересечения с осью Х.

Парабола ветвями вверх,

значит она отрицательна между корнями ,если при этом и знаменатель отрицательный,то дробь положительна. х-4∠0 х∠4

2≤ х ≤3 общий ответ 2≤ х ≤3. Теперь рассмотрим случай когда оба положительны и числитель и знаменатель.

4∠х знаменатель положительный. А числитель неотрицательный,когда х находится правее большего и левее меньшего корня.

х≤2 или 3≤х общий ответ 4∠х

ООФ 2≤ х ≤3 или 4∠х

2)Подкоренное выражение х²-9х/8х ≥0 х(х-9) ≥ 0 0 ∠ 8х

х(х-9)≥0 -это точки пересечения с осью Х.

х∠0 или 9 ∠х числитель положителен. знаменатель положителен при 0∠х общим ответом в этой части 9∠х

тепреь рассмотрим ,когда оба отрицательны.

х(х-9)≤0 0≤х≤9

знаменатель меньше нуля при х∠0 . Это должно выполняться одновременно.0∠х≤9 обратите внимание,что х строго больше 0! Поскольку делить на 0 нельзя!

Теперь можем объединить ответы. от 0 до 9 включительно рабортает нижний ответ,а после этого верхний. Значит можно просто записать ООФ : 0∠х

4,4(30 оценок)

Ответ:

elnerfaiq

02.06.2022

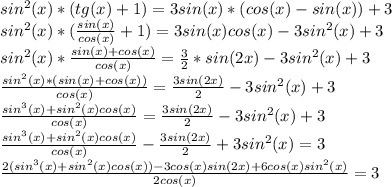
$sin^{2}(x)*(tg(x)+1)=3sin(x)*(cos(x)-sin(x))+3\\sin^{2}(x)*(\frac{sin(x)}{cos(x)} +1)=3sin(x)cos(x)-3sin^{2}(x)+3\\sin^{2}(x)*\frac{sin(x)+cos(x)}{cos(x)}=\frac{3}{2}*sin(2x)-3sin^{2}(x)+3\\\frac{sin^{2}(x)*(sin(x)+cos(x))}{cos(x)}=\frac{3sin(2x)}{2}-3sin^{2}(x)+3\\\frac{sin^{3}(x)+sin^{2}(x)cos(x)}{cos(x)}=\frac{3sin(2x)}{2}-3sin^{2}(x)+3\\\frac{sin^{3}(x)+sin^{2}(x)cos(x)}{cos(x)}-\frac{3sin(2x)}{2}+3sin^{2}(x)=3\\\frac{2(sin^{3}(x)+sin^{2}(x)cos(x))-3cos(x)sin(2x)+6cos(x)sin^{2}(x)}{2cos(x)}=3\\$

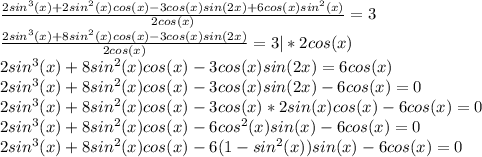
$\frac{2sin^{3}(x)+2sin^{2}(x)cos(x)-3cos(x)sin(2x)+6cos(x)sin^{2}(x)}{2cos(x)}=3\\\frac{2sin^{3}(x)+8sin^{2}(x)cos(x)-3cos(x)sin(2x)}{2cos(x)}=3|*2cos(x)\\2sin^{3}(x)+8sin^{2}(x)cos(x)-3cos(x)sin(2x)=6cos(x)\\2sin^{3}(x)+8sin^{2}(x)cos(x)-3cos(x)sin(2x)-6cos(x)=0\\2sin^{3}(x)+8sin^{2}(x)cos(x)-3cos(x)*2sin(x)cos(x)-6cos(x)=0\\2sin^{3}(x)+8sin^{2}(x)cos(x)-6cos^{2}(x)sin(x)-6cos(x)=0\\2sin^{3}(x)+8sin^{2}(x)cos(x)-6(1-sin^{2}(x))sin(x)-6cos(x)=0\\$

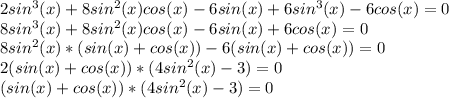
$2sin^{3}(x)+8sin^{2}(x)cos(x)-6sin(x)+6sin^{3}(x)-6cos(x)=0\\8sin^{3}(x)+8sin^{2}(x)cos(x)-6sin(x)+6cos(x)=0\\8sin^{2}(x)*(sin(x)+cos(x))-6(sin(x)+cos(x))=0\\2(sin(x)+cos(x))*(4sin^{2}(x)-3)=0\\(sin(x)+cos(x))*(4sin^{2}(x)-3)=0$