ответ: y = -6x - 11
Объяснение:
Касательная параллельна прямой y = -6x + 7. Коэффициент наклона этой прямой равен -6.
Так как касательная параллельна этой прямой, следовательно, коэффициент наклона касательной тоже равен -6.
То есть мы знаем коэффициент наклона касательной, а, тем самым, значение производной в точке касания.
Итак, у нас дана функция y = x² - 4x - 10 и значение производной в точке касания.
а) Найдем точку, в которой производная функции y = x² - 4x - 10 равна -6.
Сначала найдем уравнение производной.
y' = (x² - 4x - 10)' = 2x - 4
Приравняем производную к числу -6.
2x - 4 = -6
2x = -2
x = -1
б) Найдем уравнение касательной к графику функции y = x² - 4x - 10 в точке x₀ = -1.
Найдем значение функции в точке x₀ = -1.
y(-1) = (-1)² - 4·(-1) - 10 = 1 + 4 - 10 = -5
Подставим эти значения в уравнение касательной:
y - y(x₀) = y'(x₀)(x - x₀)
y - (-5) = -6(x - (-1))
y + 5 = -6(x + 1)
y = -6x - 6 - 5
y = -6x - 11
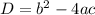(если дискриминант больше нуля уравнение имеет 2 корня, если равен нулю, уравнение имеет 1 корень, если меньше нуля, то нет корней), либо применяя разложение многочлена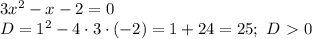
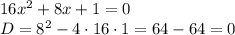
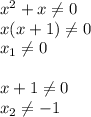
4) Если у двух равных дробей равны знаменатели, значит у них равны и числители: x^2=16; x=+-V16; x1=4; x2=-4/
1) При решении дробных уравнений обычно от дробей избавляются. Для этого находят общий знаменатель, дополнительные множители, и умножают числители на дополнительные множители, отбросив при этом знаменатель.
x^2/(x-1)=(2-x)/(x-1); x^2=2-x; x^2+x-2=0; решаем через дискриминант, получим x1=1; x2=-2.
2) (4y+3)/(y-7)=-x^2/(y-7); 4y+3=-x^2; x^2+4y+3=0; y1=3; y2=1.
3) Общий знаменатель: (х+10)(х-8). Решение: x*(x-8)=1*(х+10); x^2-8x=x+10; x^2-9x-10=0; x1=10; x2=-1.
4) Общий знаменатель: (3x-1)(27-x). Решение: 1*(27-х) =x*(3x-1); 27-x=3x^2-x; 3x^2=27; x^2=27/3; x^2=9; x=+-V9; x1=3; x2=-3.