2 см и 2 см
Объяснение:
Дан прямоугольник, периметр которого равен 8 см. Тогда сумма двух сторон равна 8:2 = 4 см. Обозначим через x одну сторону прямоугольника. Тогда вторая сторона равна: 4–x. Теперь составим функцию площади прямоугольника: y=x·(4–x)=4·x-x². Дифференцируем функцию
y'=(4·x–x²)'=4–2·x.
Находим критические точки функции:
y'=0 ⇔ 4–2·x=0 ⇔ x=2 – критическая точка.
Проверим знаки производной:
при x<2: y'=4–2·x>0 и при x>2: y'=4–2·x<0.
Значит, x=2 точка максимума. Тогда
yмакс=y(2)=4·2–2²=8–4=4 см²,
а стороны x=2 см и 4–2=2 см.
Пусть меньшая сторона — х метров, тогда большая — х+8 метров. Зная площадь площадки, составим и решим мат. модель:
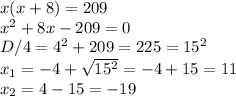
Отрицательный корень отбрасывает, т.к. длина не может быть отрицательной.
Следовательно, меньшая сторона — х = 11 метров;
большая — х+8 = 11+8 = 19 метров.
Для определения кол-ва упаковок материала для бордюра, вычислим периметр площадки:
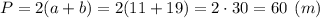
Необходимое количество упаковок равно:
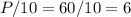
м.Большая сторона детской площадки равна: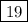 
м.Необходимое количество упаковок равно: 
.
S=2*3=6 м