1)2((8+x)+x)=20
8+2x=20:2
8+2х=10
2х=10-8
2х=2
х=2:2
х=1-ширина
8+х=8+1=9 - длина
2)2х+х=441
3х=441
х=441:3
х=147-второе число
3х=294-первое число
3)х+у+х-у=140+14
2х=154
х=154:2
х=77-первое число
77+у=140
у=140-77
у=63-второе число
4) х+(х+1)+(х+2)=201
3х+3=201
3х=201-3
3х=198
х= 198:3
х=66
х+1=67
х+2=68
Это числа 66,67 и 68
Почему я так смело возводил в квадрат? Если заметить ,то правая часть всегда неотрицательная ,а значит могу возводить и не наносить ограничения
Я привёл данную функцию к двум простейшим ,разберём их
Первая функция!
Мы знаем как выглядит модуль |2x+2| ,но мы его подняли ,а значит его вершина будет иметь координаты (-1;3)
Нам нужно одно решение с прямой x-a
Единственное решение может иметь только тогда ,когда прямая x-a касается вершины,то есть ,подставим вместо x=-1
Получаем:-1-a=3⇔-a=4⇔a=-4
Рассмотрим вторую функцию!
Если заметить ,то можно понять ,что вторая функция симметрична первой ,а значит её вершина будет иметь (-1;-3)
Делаем всё тоже самое ,подставляем x=-1
-1-a=-3⇔-a=-2⇔a=2
При а={-4;2} - будет единственное решение
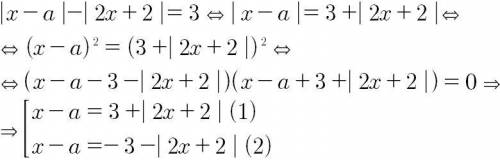
{x=35-5y
{3·(35-5y)+2y=27
{x=35-5y
{105-15y+2y=27
{x=35-5y
{-15y+2y=27-105
{x=35-5y
{-13y= - 78
{x=35-5·6
{y= 6
{x= 5
{y= 6
О т в е т. (5;6).