1)(с-2)(с+2)и2)(х³+4)(х³-4)
У першому випадку це різниця квадратів двох виразів =добутку різниці та суми цих виразів Перша формула у темі "Формули скороченого множення" виглядає у загальному так а²-b²=(a-b)(a+b)
Пояснення:
другий випадок аналогічний але ікс знаходиться в степені 3
Для того аби було ясніше уявляєш Х³ як змінну А яби побачити формулу вказану вище і виходить (А+4)(А-4)⇒А²-4²
Тепер підставляємо даний ікс у третій степені ⇒(Х³)²-4²
(Х³)² це в свою чергу тема "дії зі степенями = Х³°²=Х∧6 (ікс у 6степені)
ОТЖЕ
(х³+4)(х³-4)=х∧6-16
x = r cos(a), y = r sin(a), dx dy = r dr da, r > 0, -π < a < π
1. 0 < x < 2, 0 < y < √(4 - x^2)
r cos(a) > 0 - выполняется при cos(a) > 0: -π/2 < a < π/2
r sin(a) > 0 - выполняется при sin(a) > 0 : 0 < a < π
0 < r sin(a) < √(4 - x^2)
0 < r^2 sin^2(a) < 4 - r^2 cos^2(a)
0 < r^2 < 4 : r < 2 - необходимо и достаточно
0 < r cos(a) < 2 - достаточное условие: r < 2 (уже выполнено)
т.е. область интегрирования: 0 < a < π/2, 0 < r < 2
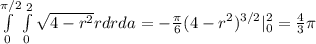
2. Область интегрирования такая же,
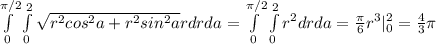
4 +5Cosx - 2(1 - Cos²x) = 0
4 +5Cosx -2 + 2Cos²x = 0
2Cos²x + 5Cosx +2 = 0
Cosx = y
2y² + 5y + 2 = 0
D = 9
y = (-5 +3)/4= -1/2
у= (-5 -3)/4 = -2
а) Cosx = -1/2
x = +-arcCos(-1/2) + 2πk , k ∈ Z
x = +-2π/3 + 2πk , k ∈ Z
б)Cosx = -2
∅
ответ: x = +-2π/3 + 2πk , k ∈ Z