150 км.
Объяснение:
Пусть s км - расстояние между пунктами . Тогда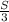 
км/ч скорость автомобиля из пункта В в С, а 
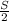км/ч скорость на обратном пути. Так как по условию на обратном пути он увеличил скорость на 25 км/ч, то составляем уравнение :
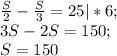
Значит расстояние между пунктами 150 км/ч.
Пусть x км/ч скорость автомобиля из пункта В в С. Тогда (x +25) км/ч - скорость на обратном пути. 3x км - расстояние между В и С, 2(x+25) км обратный путь. Составляем уравнение:
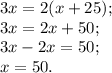
50*3=150 (км) -расстояние между пунктами .
а) х∈(-∞;-3)∪(-3;3)∪(3;+∞)
bв) р∈(-∞;-4)∪(-4;4)∪(4;+∞)
с) s∈(-∞;-2)∪(-2;2)∪(2;+∞)
d) t∈R
e) c∈(-∞;-2)∪(-2;2)∪(2;+∞)
f) а∈(-∞;-15)∪(-15;3)∪(3;+∞)
У последних двух надо решить уравнения, узнать, какие числа обращают в нуль знаменатель и выбросить из допустимых значений. т.к. делить на нуль нельзя.
4) c∈(-∞;-2)∪(-2;2)∪(2;+∞); I2cI=4⇒с=±2, значит,
c∈(-∞;-2)∪(-2;2)∪(2;+∞)
3-Iа/3+2I=0; Iа/3+2I=3; а/3+2=±2; откуда а =-15, а =3, и ответ
а∈(-∞;-15)∪(-15;3)∪(3;+∞), откуда выброшены точки -15 и 3.
остальные решаются устно. т.е. выбрасываются значения, которые обращают в нуль знаменатель.
d) t∈R, т.к. ни при каких t (t ²+36) в нуль не обратишь, это сумма неотрицательного t ² и положительного числа 36, и эта сумма положительна, т.е. допускает любое значение переменной t
х=128:32
х=4
4×32=128
128=128
(старалась как могла)