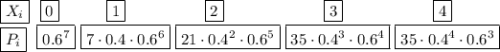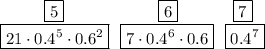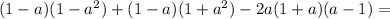
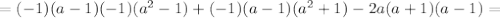
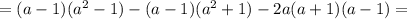
![=(a-1)[(a^2-1)-(a^2+1)-2a(a+1)]=](/tpl/images/0589/4041/5be02.png)
![=(a-1)[a^2-1-a^2-1-2a^2-2a]=(a-1)(-2a^2-2a-2)=](/tpl/images/0589/4041/5706b.png)
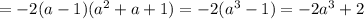
Случайная величина X распределена по биномиальному закону.
Всего n = 7 испытаний. Вероятность успеха в одном испытании равна p = 0.4, тогда q = 1 - р = 0.6
1) Вероятность того, что стрелок попадет в цель ни разу
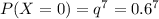
2) Вероятность того, что стрелок попадет в цель один раз
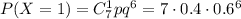
3) Вероятность того, что стрелок попадет в цель два раза
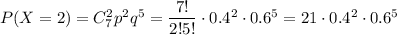
4) Вероятность того, что стрелок попадет в цель три раза
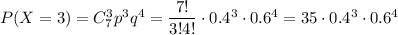
5) Вероятность того, что стрелок попадет в цель четыре раза
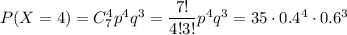
6) Вероятность того, что стрелок попадет в цель пять раз
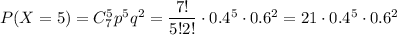
7) Вероятность того, что стрелок попадет в цель шесть раз
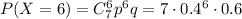
8) Вероятность того, что стрелок попадет в цель 7 раз
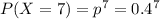
Закон распределения случайной величины X: