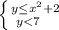
Нарисуем параболу у=х²+2, ветви вверх, вершина в точке (0,2) . Надо заштриховать область, расположенную ниже этой параболы.
Нарисуем прямую у=7, она проходит параллельно оси ОХ через точку (0,7) . Надо заштриховать область, расположенную ниже этой прямой. Так как неравенство у<7 строгое, то линия у=7 не входит в область, её рисуем штриховой линией.
Тогда область, соответствующая системе неравенств, будет та, которая получается в результате наложения штриховок. Верхняя граница этой области обведена зелёной линией.
СтранноЮ простая ведь задача, для 1 класса, даже думать не нужно, всё известно.
Гляди
Пусть
v - скорость одного, тогда
(v+1) - скорость другого, ну и всё, скорости известны, расстояние известно, найдём время
36/v - время одного
36/(v+1) - время другого, и нам известно, что первое время на полчаса больше, значит
36/v - 36/(v+1) = 1/2
72*(v+1) -72*v = v*(v+1)
v^2 + v -72 = 0
v1=8 v1+1 = 9
v2=-9 v2+1 = -8
ответ Скорость одного была 8, а второго 9 км/ч
Замечание1 Я сразу написал решение квадратного уравнения, ведь у тебя, насколько я понял, возникли сложности с решением ЗАДАЧИ, а уравнения ты решать умеешь.
Замечание2 Я специально не отбросил второй, отрицательный корень, чтобы ты увидела, что уравнение гораздо умнее, чем можно было подумать, оно даёт 2 правильных одинаковых решения(знак - это направление скорости).
Но если уж слишком по-школьному, то отрицательное решение можешь и отбросить.
Замечание3 Я не использовал термины первый и второй, а использовал один и другой, это более обще, и, вообще говоря, они у меня "наоборот" к условию. А найти нужно скорости "каждого", а не конкретно "первого" и "второго".
Ну и просто так: А зачем практически летом решать задачи про лыжников? Про велосипедистов, ну или бегунов как-то своевременнее, что ли. :)
(x-120)=(x-180)*2
x-120=2x-360
2x-360-(x-120)=0
2x-360-x+120=0
x-240=0
x=240