Найдите последнюю цифру числа: а)2004 в 2004 степени б)1936 в 537степени

👇

Ответ:

vladik1501

28.06.2022

2004^2004 4^4
4^1=4
4^2=16
4^3=64
4^4=256 ⇒
2004^2004 оканчивается на цифру 6.
1936^537 6^7
6^1=6
6^2=36
6^3=216
6^4=1296 ⇒
1936^537 оканчивается на цифру 6.

4,6(75 оценок)

Открыть все ответы

Ответ:

astasevbogdanp08dn2

28.06.2022

1)y/y^2-9 - 3/9-y^2 = y /y^2-9 - (-3/y^2-9) = y /y^2-9 + 3/y^2-9 = y+3/(y-3)(y+3)= 1/y-3

2)2x/x^2-4 - 4/4 - x^2 =2x/x^2-4 - (-4/x^2-4) = 2x+4/x^2-4 = 2(x+2)/(x-2)(x+2)= 2/x-2

3)x2/x-7 + 7x/7-x = x^2/x-7 - 7x/x-7 = x^2-7x/x-7 = x(x-7)/x-7= x

4)7/x^2-9x + 3x-7/x^2-9x =7+3x-7/x^2-9x= 3x/x^2-9x

5)5y-19/11y + 6y+8/11y =5y-19+6y+8/11y= 11y - 27/11y

6)y+3/y-3 - 9-y/y-3 =y+3-9-y/y-3=-3/y-3

7)12a+b/28a - b-30a/28a =12a+b-b-30a/28a = -28a/28a = -1

8)6a-4/2 - 2-3a/2 =6a-4-2-3a/2 = 3a+6/2 = 3(a+2)/2

9)b/a-b - a/a-b =-a/a-b - b/a-b = -(a-b)/a-b = -1

10)5a/a-b - 5b/a-b =5a-5b/a-b = 5(a-b)/a-b = 5

11)m^2/m-5 - 25/m-5 =m^2-25/m-5 = (m-5)(m+5)/m-5= m+5

12)a^2-47/a+7 - 2/a+7 =a^2-47-2/a+7 = a^2-49/a+7 = (a-7)(a+7)/a+7=a-7

13)m/m^2-n^2 - n/m^2-n^2 =m-n/m^2-n^2= m-n/(m-n)(m+n)=1/m+n

14)m2/m+n - n^2/m+n =m^2-n^2/m+n = (m-n)(m+n)/m+n = m-n

15)n^2/3n+3m - m^2/3n+3m =n^2-m^2/3n+3m = (n-m)(n+m)/3(n+m) = n-m/3

4,5(20 оценок)

Ответ:

dan355

28.06.2022

Сначала нужно выполнить чертеж (смотрите рисунок). Вообще говоря, при построении чертежа в задачах на площадь нас больше всего интересуют точки пересечения линий. Найдем точки пересечения параболы y=4-x² и прямой y=2-x. Это можно сделать двумя
Первый это посмотреть на график где линии пересекаются, второй это аналитический В данном случае можно воспользоваться графическим так как на графике ясно видно, что парабола и прямая пересекаются в точке (-1 ; 3) и (2 ; 0).Но бывают случаи, когда точкой пересечения будет, например, точка (-3,14 ; 1), тогда графически вы не сможете определить точки пересечения, в таком случае используется аналитический метод.
Попробуем применить аналитический для вычисления точек пересечения. Для этого мы приравниваем уравнения y=4-x² и y=2-x
4-x²=2-x
x²-x+2-4=0
x²-x-2=0
применим теорему Виета для решения квадратного уравнения
x₁+x₂=1
x₁x₂= -2
x₁=2
x₂= -1

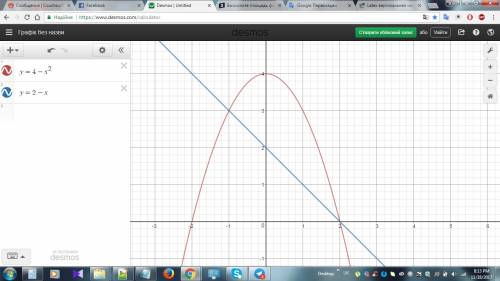
Теперь посмотрим где расположена фигура. Нам важно, какой график выше (относительно другого графика), а какой – ниже.

Из графика видно, что выше расположена парабола y=4-x² , а ниже прямая y=2-x.

Формула для вычисления площади: 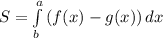$S= \int\limits^a_b {(f(x)-g(x))} \, dx$ где f(x) это функция которая расположена выше, чем функция g(x)

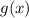
таким образом для исчисления площади нужно взять интеграл

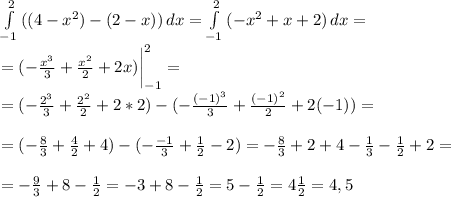
$\int\limits^2_{-1} {((4- x^{2} )-(2-x))} \, dx = \int\limits^2_{-1} {(-x^{2} +x+2)} \, dx = \\ = (-\frac{x^3}{3} +\frac{x^2}{2} +2x) \bigg|^2_{-1}= \\ =(-\frac{2^3}{3} +\frac{2^2}{2} +2*2) -(-\frac{(-1)^3}{3} +\frac{(-1)^2}{2} +2(-1)) = \\ \\ =(-\frac{8}{3} +\frac{4}{2}+4) -(-\frac{-1}{3} +\frac{1}{2} -2) = -\frac{8}{3} +2+4- \frac{1}{3} -\frac{1}{2} +2= \\ \\ = -\frac{9}{3} +8-\frac{1}{2} =-3+8- \frac{1}{2}=5- \frac{1}{2}=4 \frac{1}{2}=4,5$