1) Точки экстремума - это точки, в которых производная = 0 или не существует.
Значит, надо искать производную. Сработает формула:
(U/V)' = (U'V - UV')/V²
Начнём.
y'= (-2(x+1) - (3-2x) )/(x+1)² = -5/(х+1)²
Эта производная не равна нулю. Но при х = -1 она не существует.
ответ: х = -1 это точка разрыва.
2)план наших действий:
ищем производную
приравниваем к нулю и решаем уравнение;
Смотрим, какие корни попали в указанный промежуток;
ищем значения функции в этих точках и на концах промежутка;
пишем ответ.
Поехали?
y'= -2/(х² +4)² * 2х= -4х/(х² +4)²
-4х/(х² +4)² = 0, ⇒ х = 0; 0∈[-10;10]
a) x = 0
y = 2/4 = 0,5
x = -10
y = 2/104
х = 10
у = 2/104
ответ: max y = 0,5
min y = 2/104 = 1/52
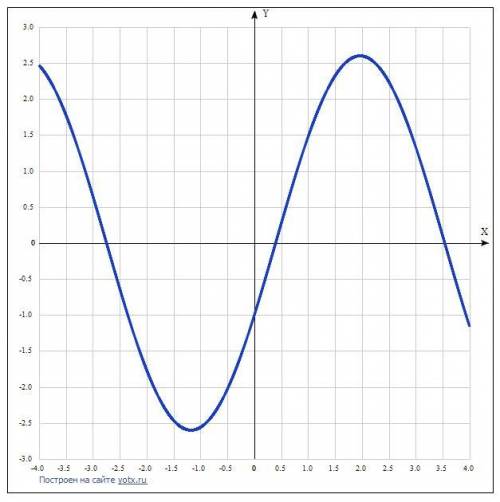
Чтобы найти множество значений функции y=2,4sin x - cos x, надо определить экстремумы функции.
Производная равна y' = 2,4cos x + sin x.
Приравняем нулю производную: 2,4cos x + sin x = 0.
Разделим левую и правую части равенства на coscos x x, если он не равен 0 (это проверится далее).
2,4(cos x/cos x) + (sin x/cos x) = 0,
tg x = -2,4.
Отсюда получаем точки экстремума:
x = arc tg(-2,4) = arc tg(-12/5) = πn - 1,176005, n ∈ Z.
При n = 0 точка экстремума в отрицательной области х = -1,176005.
При n = 1 точка экстремума в положительной области:
х = 3,141593 - 1,176005 = 1,965588.
Для получения значения функции в точках экстремума подставим значение аргумента в уравнение функции.
y=2.4sin(-1,176005) - cos(-1,176005) = -2,6.
y=2.4sin(1,965588) - cos(1,965588) = 2,6.
Получили ответ: множество значений функции
y=2,4sinx-cosx (-2,6; 2,6).