![\frac{7p-35}{15-3p} = \frac{7*p-7*5}{(-3)*(-5)+(-3)*(p)}= \frac{7*(p-5)}{(-3)*[(-5)+(p)]}= \frac{7*(p-5)}{(-3)*(-5+p)}=](/tpl/images/0592/1551/12dad.png)
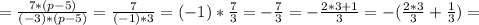
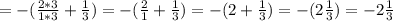
3) y = -1; 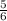 ; 1
; 1
4) Нет корней
Объяснение:
3) Прибавим левые и правые части уравнений системы:
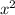 + 7xy + 9
+ 7xy + 9 - xy = 10 - 6
- xy = 10 - 6
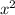 + 6xy + 9
+ 6xy + 9 = 4
= 4
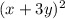 = 4
= 4
x + 3y = 2 x + 3y = -2
1) x = 2 - 3y 2) x = -3y - 2
По очереди подставим получившиеся значения х во второе уравнение:
1) 9 - (2 - 3y)y = 10
- (2 - 3y)y = 10
9 - 2y + 3
- 2y + 3 = 10
= 10
12 - 2y - 10 = 0
- 2y - 10 = 0
6 - y - 5 = 0
- y - 5 = 0
Решим через дискриминант:
a = 6 b = -1 c = -5
D = 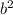 - 4ac = 1 + 120 = 121 =
- 4ac = 1 + 120 = 121 = 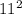
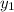 =
= 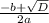 =
= 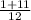 = 1
= 1
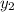 =
= 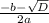 =
= 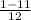 =
= 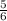
2) 9 - (- 3y - 2)y = 10
- (- 3y - 2)y = 10
9 + (3y + 2)y = 10
+ (3y + 2)y = 10
9 + 2y + 3
+ 2y + 3 = 10
= 10
12 + 2y - 10 = 0
+ 2y - 10 = 0
6 + y - 5 = 0
+ y - 5 = 0
Решим через дискриминант:
a = 6 b = 1 c = -5
D = 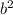 - 4ac = 1 + 120 = 121 =
- 4ac = 1 + 120 = 121 = 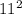
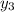 =
= 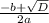 =
= 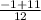 =
= 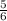
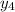 =
= 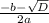 =
= 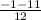 = -1
= -1
Корень 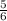 повторяется, а значит мы получили 3 различных корня:
повторяется, а значит мы получили 3 различных корня:
y = -1; 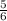 ; 1
; 1
4)
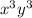 -
-  = -54
= -54
 = -18
= -18
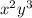 (x - y) = -54
(x - y) = -54
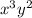 (x - y) = -18 => 3
(x - y) = -18 => 3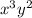 (x - y) = -54
(x - y) = -54
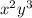 =
= 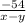
3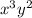 =
= 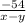
Следовательно:
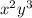 = 3
= 3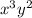
3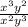 = 0
= 0
ОДЗ: х≠0, у≠0
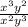 = 0
= 0
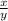 = 0
= 0
х = 0
Противоречие ОДЗ, значит система корней не имеет.
Объяснение:
z = xy, при условии 1/x + 1/y = 4
Выразим y через x:
1/y = 4 - 1/x = (4x - 1)/x
y = x/(4x - 1)
z = xy = x^2/(4x - 1)
Область определения z: x ≠ 0; y ≠ 0; x ≠ 1/4
Находим производную теперь уже функции одной переменной.
z ' = [2x(4x - 1) - x^2*4] / (4x-1)^2 = (8x^2 - 2x - 4x^2) / (4x-1)^2 = (4x^2 - 2x)/(4x-1)^2
В точке экстремума производная, то есть ее числитель, равна 0.
4x^2 - 2x = 0
2x(2x - 1) = 0
Так как x ≠ 0, то:
2x - 1 = 0
x = 1/2; y = x/(4x - 1) = (1/2) / (4/2 - 1) = 1/2
z = xy = (1/2)*(1/2) = 1/4.
В точке x = 1 > 1/2 будет z ' = (4 - 2)/(4 - 1)^2 = 2/3^2 = 2/9 > 0
Значит, при x > 1/2 функция растет.
В точке x = 1/3 < 1/2 будет z ' = (4/9 - 2/3) / (4/3 - 1)^2 = (-2/9) / (1/3)^2 = -2 < 0
Значит, при x < 1/2 функция падает.
Точка (1/2; 1/2; 1/4) - точка минимума.