а) если х=0, то у=5; ели х=1, то у=5-1=4
ответ (0;5), (1;4)
в)а) если х=0, то у=-1/3; ели х=-1, то у=-1
ответ (0;-1/3), (-1;-1)
д) можно свернуть по формуле (х+у)²=25⇒х+у=±5
Если х=0, то у=±5; если у=0, то х=±5
ответ (0;5),(0;-5),(5;0),(-5;0)
б) выразим у=5-3х, так проще подбирать решения. если х=0, то у=5, если х=1, то у=2
ответ (0;5),(1;2)
г) х²+у²=9, если х=0, у=±3, если у=0, то х=±3
ответ (0;3),(0;-3),(3;0),(-3;0)
е) х²-ху=0; х*(х-у)=0, если х=0, то у - любое число. скобка равна нулю, когда х=у, например, х=3;у=3; х=2;у=2 и т.д.
ответ (0;35),(0;-3),(3;3),(2;2)
Объяснение:
2)-0,2х+0,4у=1
-0,2х=1-0,4у умножим на -1, чтобы избавиться от минуса перед х:
0,2х=0,4у-1/0,2 разделим на 0,2, чтобы избавиться от коэффициента перед х:
х= 2у-5 ответ№2
3)В системе, состоящей из уравнений:
5х-9у=38
3х+2у=8
для решения методом сложения нужно: ответ №2:
(5х-9у=38)*3 = 15х-27у=114
(3х+2у=8)*(-5)= -15х-10у= -40
4)Систему, состоящую из уравнений:
2х-3у= -1;
х-5у=3 удобнее решить методом подстановки.
5) Решением системы, состоящей из уравнений:
4х-3у=-11;
10х+5у=35
является: (1; 5)
Подставляем поочерёдно в уравнения заданные значения х и у, левая и правая части уравнений должны быть равны.
Только последняя пара дала результат -11= -11 и 35=35
1)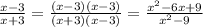
2)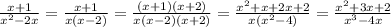
3)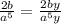
4)
5)
6)
7)