В решении.
Объяснение:
Решить систему уравнений графически:
3х + у = 1
у + х = 5
Построить графики. Графики линейной функции, прямые линии. Придать значения х, подставить в уравнение, вычислить у, записать в таблицу. Для построения прямой достаточно двух точек, для точности построения определить три.
Прежде преобразовать уравнения в уравнения функций:
3х + у = 1 у + х = 5
у = 1 - 3х у = 5 - х
Таблицы:
х -1 0 1 х -1 0 1
у 4 1 -2 у 6 5 4
По вычисленным точкам построить две прямые.
Координаты точки пересечения графиков: (-2; 7).
Решение системы уравнений: (-2; 7).

Объяснение:
Квадратичная функция: f(x) = ax²+ bx + c
Дана функция:
f(x) = 3 + 2x - x² или f(x) = -x² + 2x +3
- парабола, ветви вниз (a<0)
Найдем координаты вершины:
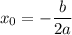 - ось симметрии.
- ось симметрии.
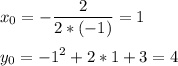
⇒ координаты вершины (1; 4)
Пересечение с осями:
1) с осью 0у ⇒
х = 0; у = 3.
2) с осью 0х ⇒
у=0; -х² +2х +3 = 0
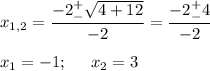
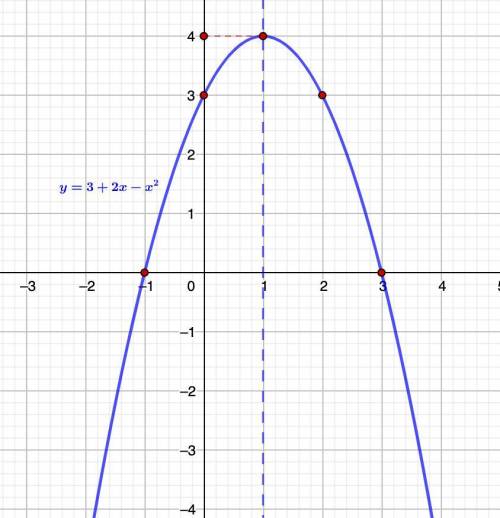
Строим график (см. рис)
По графику определим:
1) f(x) > 0 (часть графика выше оси 0х)
f(x) > 0 при х ∈ (-1; 3)
f(x) < 0 (часть графика ниже оси 0х)
f(x) < 0 при х ∈ (-∞; -1) ∪ (3; +∞)
2) Область значения функции
Е(у) : y ∈ (-∞; 4]
3) Промежутки возрастания и убывания функции:
Возрастает (при увеличении значений х, значения у тоже увеличиваются) при
х ∈ (-∞; 1]
Убывает (при увеличении значений х, значения у уменьшаются) при
х ∈ [1; +∞)
2)0.16*0,5=0,08
3)5-0,08=4,92
4)1,5*4,92=7,38
5)8,5+7,38=15,88
15,88=