Question

По двум взаимно перпендикулярным прямым движеутся равномерно две точки. сейчас они обе находятся в точке пересечения прямых, а через 10 с расстояние между ними будет 1м. найдите скорость каждой точки, если одна из них
проходит за 3с столько же, сколько другая проходит за 4 с.

Answer 1

Пусть х и у - скорости точек. Тогда из условия имеем систему: (1 м = 100 см)

$(10x)^2+(10y)^2=10000;$

$3x=4y.$

Выражаем у через х из второго и подставляем в первое:

$y=\frac{3x}{4};$

$x^2+\frac{9x^2}{16}=100.$

Отсюда:

$x^2=\frac{16}{25}*100$

х = 8 см/с;   у = 6 см/с.

ответ: 8 см/с;  6 см/с.

Answer 2

3/4=0,75; 1^2=1

Пусть х м/с - скорость одной точки, тогда скорость другой 0,75х м/с. За 10 секунд первая пройдёт расстояние 10х метров, а вторая - 0,75х*10=7,5х метров. По теореме Пифагора расстояние между ними будет 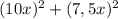$(10x)^2+(7,5x)^2$ или 1 метр.

Составим и решим уравнение:

$(10x)^2+(7,5x)^2=1$

$100x^2+56,25x^2=1$

$156,25x^2=1$

$x^2=\frac{1}{156,25}$

$x^2=0,0064$

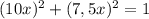
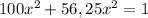
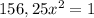
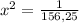
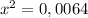
Так как скорость - положительное число, то

х=0,08

0,75х=0,75*0,08=0,06

ответ: одна из точек движется со скоростью 0,08 м/с, а другая - 0,06 м/с.