Объяснение:
1)
arccos (2x-3)=\frac{\pi }{3}arccos(2x−3)=
3
π
Так как cos(arccosx) = x, |x| \leq 1cos(arccosx)=x,∣x∣≤1 , то
\begin{gathered}2x-3 = cos\frac{\pi }{3} ;\\2x-3 = \frac{1}{2} ;\\2x=0,5+3;\\2x=3,5;\\x=3,5:2;\\x=1,75.\end{gathered}
2x−3=cos
3
π
;
2x−3=
2
1
;
2x=0,5+3;
2x=3,5;
x=3,5:2;
x=1,75.
ответ: 1,75.
2)
\begin{gathered}arccos (x+\frac{1}{3} ) =\frac{2\pi }{3} ;x+\frac{1}{3} = cos \frac{2\pi }{3} ;x+\frac{1}{3} = -\frac{1}{2} ;x=-\frac{1}{2}-\frac{1}{3};x= -\frac{5}{6} .\end{gathered}
arccos(x+
3
1
)=
3
2π
;
x+
3
1
=cos
3
2π
;
x+
3
1
=−
2
1
;
x=−
2
1
−
3
1
;
x=−
6
5
.
ответ: -\frac{5}{6} .−
6
5
.
1) - x2 - 6x + 27 = 0
x2+6x-27=0
D=36+108=144
x1=(-6+12)/2=3
x2=(-6-12)/2=-9
2) - x2 - 97x - 630 = 0;
x2+97x+630=0
D=97^2-4*630=6889
x1=(-97+83)/2=-7
x2=(-97-83)/2=-90
3) x2 + 12x + 36 = 0
D=12^2-4*36=0
x=-12/2=-6
4) x2 - 3x + 17 = 0;
D=3^2 -4*17=-59
x1=(3+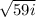 )/2=
)/2=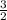 +
+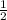
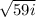
x2=(3-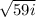 )/2=
)/2=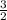 -
-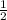
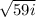
5) x2 - 36x + 324 = 0;
D=(-36)2 - 4·1·324=0
x=36/2=18
6) x2 - 58x + 832 = 0
D=(-58)2 - 4·1·832=36
x1=(58+6)2=32
x2=(58-6)/2=26
7) x2 - 16x - 17 = 0;
D=(-16)2 - 4·1·(-17)=324
x1=(16+18)/2=17
x2=(16-18)/2=-1
8) x2 + 15x + 56 = 0
D=152 - 4·1·56=1
x1=(-15+1)/2=-7
x2=(-15-1)/2=-8
х=-78:26
х=-3
б) 0,2х=2,8
х=2,8:0,2
х=14
в) -1/3х=24
х=24/1:(-1/3)
х=24/1*(-3/1)
х=24*(-3)
х=-72