1- sin квадрат х - sin квадрат х = корень 3 делить на 2
2 sin квадрат х = (2- корень из 3)/2
sin квадрат х= (2-корень из 3)/4
sin х= +-корень из ((2-корень из 3)/4)
х=арксинус от +-корень из ((2-корень из 3)/4)
надо проверить попадает ли хотя бы один корень в область значений [-1;1]
корень из ((2-корень из 3)/4) 1 возводим обе части неравенства в квадрат
(2-корень из 3)/4 1 умножаем обе части на 4
2-корень из 3 4 вычитаем 4 прибавляем корень из трех
-2 корень из трех
очевидно что
-2 < корень из трех
значит
корень из ((2-корень из 3)/4) <1
значит корни попали в область определения ф-и.
Чтобы оценить периметр исходного треугольника, нужно сложить заданные неравенства
2,3 ≤ a ≤ 2,4
3,2 ≤ в ≤ 3,3
4,5 ≤ c ≤ 4,6
2,3+3,2+4,5 ≤ a+в+с ≤ 2,4+3,3+4,6
10 ≤ P ≤ 10,3
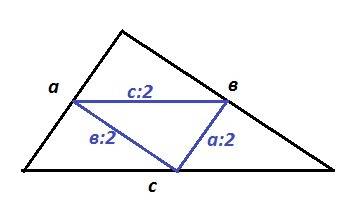
Соединили середины сторон, то есть провели 3 средние линии треугольника. Каждая средняя линия равна половине стороны, которой параллельна. Значит, периметр образованного треугольника равен половине периметра исходного треугольника
10 ≤ P ≤ 10,3 | : 2
10:2 ≤ P:2 ≤ 10,3 :2
5 ≤ P₁ ≤ 5,15
ответ : периметр полученного треугольника в пределах от 5 см до 5,15 см включительно.