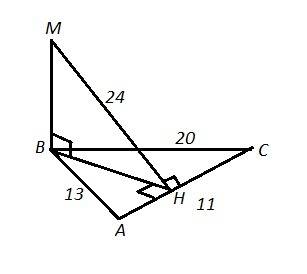
ΔАВС , АВ=13 , АС=11 , ВС=20
Наименьший угол в треугольнике лежит против наименьшей стороны,
то есть ∠В - наименьший, сторона АС=11 - наименьшая.
ВМ ⊥ пл. АВС ⇒ ВМ ⊥ любой прямой , лежащей в пл. АВС, в том числе и высоте треугольника ВН, ВН ⊥ АС.
Тогда по теореме о трёх перпендикулярах МН⊥АС (ВН - проекция МН на пл. АВС) ⇒ МН=24.
Найдём ВН , используя две формулы нахождения площади ΔАВС.
S(ABC)=1/2*АС*ВН ⇒ ВН=2S/АС .
Полупериметр р=1/2*(11+13+20)=22 ,
S=√p*(p-a)(p-b)(p-c)=√(22*11*9*2)=66 .
ВН=2*66/11=12 .
ΔВМН: ∠МВН=90° , ВМ=√(МН²-ВН²)=√(24²-12²)=√432=12√3
первое выражение: 5c^2 + 10c = 5*9 + 10*(-3) = 45 - 30 = 15
второе выражение: 4 * (-3) (-3 - 4) = - 12 * - 7 = 84
84 > 15
Значит 5с(с +2) < 4c (c -4)