выпишем координаты данных векторов:
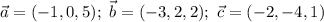
a)
координаты:
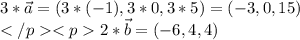
скалярное произведение векторов - число:
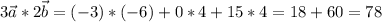
б)
координаты:
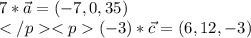
векторное произведение векторов - вектор, находим его координаты:

находим модуль(длину) полученного вектора:
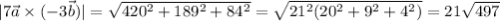
в)
координаты:
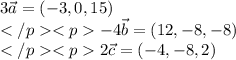
смешанное произведение векторов - число, находим его:
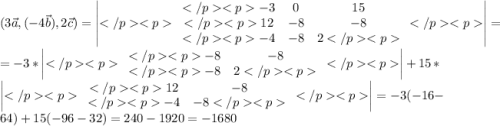
г)
Координаты:
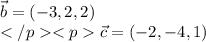
Векторы коллинеарны, если их соответствующие кординаты пропорциональны
Проверим это утверждение:
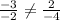
Данное равенство неверно, значит векторы b и c не коллинеарны
Векторы ортогональны, если их скалярное произведение равно нулю.
Проверим это утверждение:
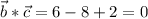
- верно, значит данные векторы ортогональны
Векторы b и c ортогональны
д)
Координаты:
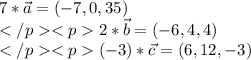
Три вектора компланарны, если их смешанное произведение равно нулю.
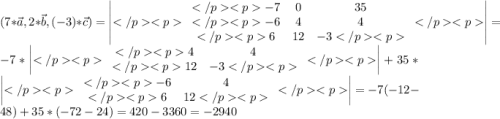
-2940 не равно нулю => данные векторы не компланарны.
выпишем координаты данных векторов:
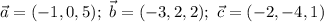
a)
координаты:
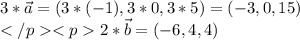
скалярное произведение векторов - число:
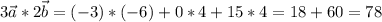
б)
координаты:
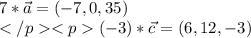
векторное произведение векторов - вектор, находим его координаты:

находим модуль(длину) полученного вектора:
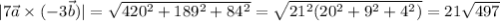
в)
координаты:
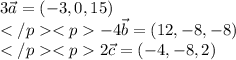
смешанное произведение векторов - число, находим его:
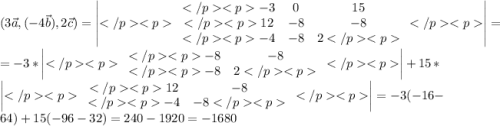
г)
Координаты:
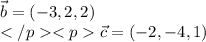
Векторы коллинеарны, если их соответствующие кординаты пропорциональны
Проверим это утверждение:
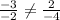
Данное равенство неверно, значит векторы b и c не коллинеарны
Векторы ортогональны, если их скалярное произведение равно нулю.
Проверим это утверждение:
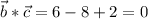
- верно, значит данные векторы ортогональны
Векторы b и c ортогональны
д)
Координаты:
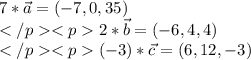
Три вектора компланарны, если их смешанное произведение равно нулю.
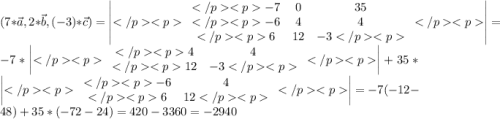
-2940 не равно нулю => данные векторы не компланарны.
3*3=9
3*3*3=27
3*3*3*3 = 81
3*3*3*3*3 = 243
Вот теперь посмотри на последние цифры:
3;9;7;1;3;9;7;1;...
через каждые 4 цифры идёт повтор.
А теперь наше число: 3^27= 3^24 * 3^3
так что на конце 1
Теперь со вторым числом:
4
4*4 = 16
4*4*4= 64
4*4*4*4 = 256
Так что видно, что через каждые 2 цифры последние повторяются: либо 4 , либо 6
4^50 оканчивается 6
Ну а сумма оканчивается на 7