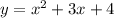
Найдем уравнение касательной, проходящей через точку с абсциссой 
Для этого найдем производную данной функции:
Найдем значение функции в точке с абсциссой :
Найдем значение производной данной функции в точке с абсциссой :
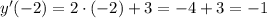
Уравнение касательной имеет вид:
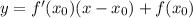
Подставим значение 
Итак, уравнение касательной заданной функции: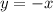 
Воспользуемся геометрическим смыслом касательной: коэффициент наклона 
касательной 
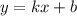численно равен тангенсу угла наклона 
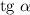с положительным направлением оси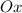 
В найденной касательной коэффициент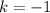 
, следовательно, 
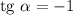при 
или 
ответ: или
Объяснение:
x²-3x<0
x(x-3)<0
Допустим:
x₁=0; x-3=0; x₂=3
Проверка при x₁>0 и x₂>3: 4²-3·4<0; 16-12<0; 4>0 - неравенство не соблюдается.
Проверка при x₁<0 и x₂<3: (-1)²-3·(-1)<0; 1+3<0; 4>0 - неравенство не соблюдается.
Проверка при x₁>0 и x₂<3: 1²-3·1<0; 1-3<0; -2<0 - неравенство соблюдается.
Следовательно, 0<x<3⇒x∈(0; 3).
/\
0/\3x
x²-7x-30≥0
Допустим:
x²-7x-30=0; D=49+120=169
x₁=(7-13)/2=-6/2=-3
x₂=(7+13)/2=20/2=10
Проверка при x₂>10: 11²-7·11-30≥0; 121-77-30≥0; 14>0 - неравенство соблюдается; при x₁>-3: 0²-7·0-30≥0; -30<0 - неравенство не соблюдается.
Проверка при x₁<-3: (-4)²-7·(-4)-30≥0; 16+28-30≥0; 14>0 - неравенство соблюдается.
Следовательно, -3>x>10⇒x∈(-∞; -3]∪[10; +∞).
\ /
\-310/x
