Данное двойное неравенство равносильно системе двух квадратных неравенств:
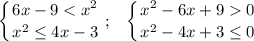
Первое неравенство  .
.
Заметим, что в левой части скрывается квадрат разности (формула  ):
): 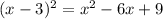 .
.
Неравенство принимает следующий вид: 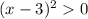 .
.
Так как квадрат числа всегда неотрицательный, то нам не подходит всего лишь один случай: 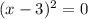 и
и 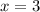 .
.
Значит, первой неравенство эквивалентно тому, что 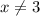 .
.
Второе неравенство 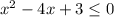 .
.
Вс уравнение 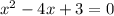 имеет по теореме Виета (утверждающей, что
имеет по теореме Виета (утверждающей, что 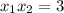 и
и 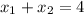 ) корни
) корни 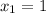 и
и 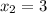 .
.
Из этого следует разложение левой части на множители: 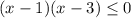 .
.
Метод интервалов подсказывает решение ![x \in [ 1; 3 ]](/tpl/images/1227/3957/60bcc.png) .
.
+ + + - - - + + +
_________![[ \; 1 \; ]](/tpl/images/1227/3957/d73a9.png) _________
_________![[ \; 3 \; ]](/tpl/images/1227/3957/abab5.png) _________
_________
\\\\\\\\\\\\\\\\\\\\\
Значит, второе неравенство равносильно тому, что  .
.
Имеем значительно более простую систему неравенств:

Вполне понятно, что ее решением является 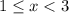 (как пересечения двух промежутков).
(как пересечения двух промежутков).
Или же 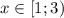 .
.
Задача решена!
ответ: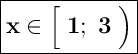
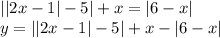
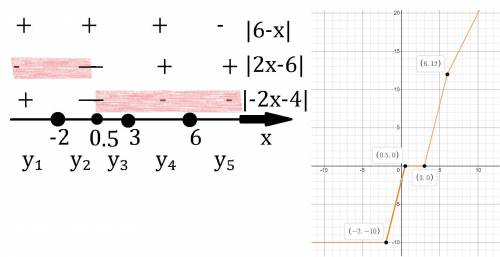
Это функция представляет из себя ломанную, нам надо найти нули этой функции. На числовой прямой отметим точки в которых аргументы модулей равны нулю. Таким образом мы сможем узнать как на промежутках раскрываются модули и выглядит функция, сверху напишу модули, чтобы было понятно, хотя можно сразу писать конечную функцию для промежутка. см. вниз.
Да и ||2x-1|-5| я представил как |2x-6| и |-2x-4|, при этом первый существует когда x>0.5, а другой когда x<0.5 т.к. 2x-1=0 =>x=0.5
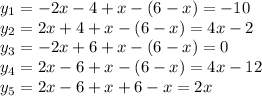
Ординаты точек в которых происходит смена знака у модуля.
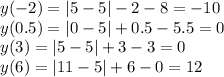
Можно построить график ломанной, а можно сразу по условию определить где функция будет равна 0.
Главное помнить, что функция 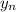 существует на каком-то промежутку, а не при всех х.
существует на каком-то промежутку, а не при всех х.
ответ: x∈[0.5;3].
Поскольку каждый следующий элемент однозначно определяется предыдущим, то как только в последовательности встретится число, которое уже было раньше, последоватеьлность с этого места начнет повторяться. Такой момент наступает на 16-ом элементе: число 89 уже было на 8-м месте. Итак, до начала периодичности записано 7 элементов: 2016, 41, 17, 50, 25, 29, 85, а после этого последовательность из 8 элементов 89, 145, 42, 20, 4, 16, 37, 58 циклически повторяется. Т.к. 2016-7=2009=8*251+1, то после семи первых элементов в 2009 элементов укладывается 251 полный период длиной 8, и поскольку остаток равен 1, то 2016-ый элемент равен первому элементу в периоде, т.е. 89. ответ: 89.