ответ: 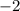 .
.
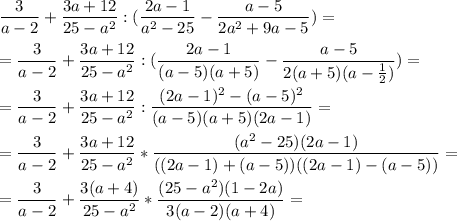
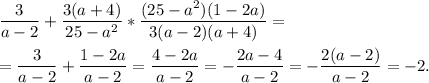
1. log^2 3(x)-15log27(x)+6=0
log^2 3(x)-5log3(x)+6=0
log3(x)=t
t^2-5t+6=0
t1+t2=5 t1=2
t1*t2=6 t2=3
log3(x)=2 log3(x)=3
x=3^2 x=3^3
x=9 x=27
2. 10(log^2)16(x)+3log4(x)-1=0
10/4 log^2 2(x)+3/2 log2 (x)-1=0
log2(x)=t
10/4 t^2+3/2 t-1=0
5 t^2+3 t-2=0
по формуле нахождения корней квадратного ур-я находим корни
t1=2/5 t2=-1
log2(x)=2/5 log2(x)=-1
x=2^2/5 x=2^ -1
x=5√4 x=1/2
только это не пять корней из четырех а корень пятой тепени из четырех, просто не знала как написать
85 км/ч
Объяснение:
пусть х - скорость второго автомобиля, а у - время, за которое он приехал к финишу
тогда скорость первого - х+25, а время - у-3
составим систему уравнений:
{612/х = у
{612/(х+25) = у-3
{ху = 612
{(х+25)(у-3) = 612
выразим х из первого уравнения:
х=612/у
подставим во второе, чтобы найти у:
(612/у + 25) (у-3) = 612
раскроем скобки:
612/у*у + 612/у *(-3) + 25у +25*(-3)=612
612 -1836/у +25у -75 =612
-1836/у + 25у = 612-612+75
-1836/у+25у =75
избавимся от знаменателя, для этого умножим все на у
-1836 + 25у^2 = 75у
25у^2 - 75у -1836 = 0
выразим -75у в виде разности:
25у^2 +180у -255у -1836=0
вынесем общий множитель за скобки:
5у(5у+36) - 51(5у + 36) =0
(5у+36) (5у-51) = 0
найдём у1:
5у+36=0
5у=-36
у=-36/5 не может быть, т.к. время не может быть отрицательным
найдём у2:
5у-51=0
5у=51
у=10,2
теперь, зная у, найдём х:
х=612/10,2=60
значит скорость второго - 60 км/ч
скорость первого на 25 больше (по условию)
60+25=85
проверим:
612:85= 7,2 (ч) - время первого
612:60= 10,2 (ч) - время второго
10,2-7,2=3 (ч) - на столько первый приехал раньше
значит решено верно!
ответ: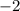 .
.
Объяснение: