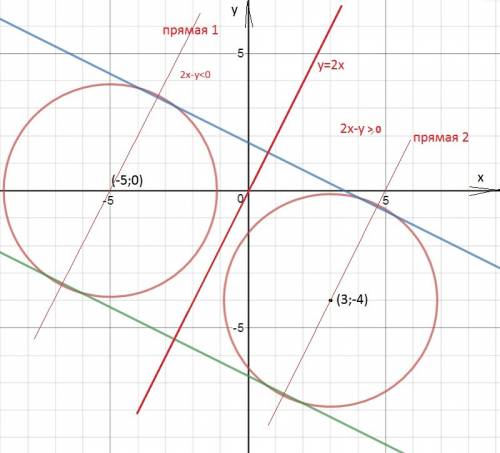
подставим 4а во второе уравнение системы. получим 4ху=2х²+2у²-2, упростим
-2ху+х²+у²=1; (х-у)²-1=0; (х-у-1)*(х-у+1)=0; 1)х=у+1 или 2)х=у-1 получили две прямые.
Если х=у+1,то 4у*(у+1)+2=а; 4у²+4у+2=а; (2у+1)²=а-1; Если а=1 ,то получим один корень, если а>1, то два корня. Если а<1, то корней нет.
Если рассмотреть первое уравнение, то при каждом a ≠ 0 — уравнение окружности c центром (0, 0) и радиусом а√2, тогда система при а=0 имеет единственное решение и поэтому не удовлетворяет условию задачи. При а≤0 уравнение не имеет смысла.
используем теперь результат выше и уточним ответ на задачу.
Если х=у+1, то у²+у²+2у+1=2а,у²+у+1/2=а; (у+1/2)²=а-1/4, при а=1/4 уравнение имеет одно решение, а при а >1/4 два различных решения.
Если х=у-1, то у²+у²-2у+1=2а,у²-у+1/2=а; (у-1/2)²=а-1/4, при а=1/4 уравнение имеет одно решение, а при а >1/4 два различных решения.
Число кратно 3, если cумма цифр числа кратна 3.
Число кратно 4, если две последние цифры числа кратны 4.
Рассмотрим условия по порядку.
1) Произведение цифр.
Разложим 24 на множители.
24=2·2·2·3.
Получены 4 цифры, а нужно получить пять.
Если мы добавим цифру 1 в произведение, то результат не изменится:
24 = 1·2·2·2·3.
Итого, имеем 5 цифр, из которых можно составить пятизначное число.
Первое условие выполнено.
2) Условие - число кратно 3
Признак делимости на 3: На 3 делятся те и только те числа, сумма цифр которых кратна 3.
Возможны варианты
Цифры числа 1; 2; 2; 2; 3.
Сумма цифр 1+2+2+2+3=10 не кратна 3.
Цифры числа 1;1; 2; 3; 4
Сумма цифр 1+1+2+3+4= 11 не кратна 3.
Цифры числа 1;1;1; 4; 6
Сумма цифр 1+1+1+4+6= 13 не кратна 3.
Цифры числа 1;1;1; 3; 8
Сумма цифр 1+1+1+3+8= 14 не кратна 3.
Других вариантов нет.
О т в е т. Нет такого числа