у=2(х-2)*-1
у=(2х-4)*-1
у=-2х+4
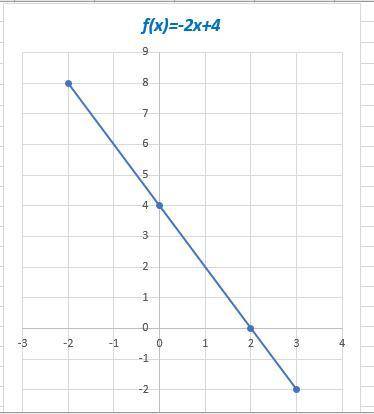
f(x)=-2x+4 - линейная функция, график - прямая
Область определения D(f) x∈R (множество всех действительных чисел)
Множество значений E(f) y∈R я
Нет максимума и минимума, непериодическая (непрерывна), ни четная, ни нечетная.
k=-2 => k<0 - функция убывающая, график образует тупой угол с положительным направлением оси 0Х.
График строится по 2-м точкам.
Можно найти точки пересечения графика с осями координат и построить график по ним.
Пересечение с осью 0Х: х=0 => y=-2*0+4=4 (0;4)
Пересечение с осью 0У: y=0 => х=-4/-2=2 (2;0)
Квадратный корень имеет смысл, если его подкоренное выражение неотрицательно. Пользуясь этим правилом, можем сказать, что подкоренное выражение должно быть больше или равно 0. Отсюда следует неравенство:
x+7.6 ≥ 0
x ≥-7.6
Видим, что наименьшее целое число, это -7
2)Поскольку графики пересекаются, то имею полное право приравнять их формулы, и найти x, это и будет абсцисса точек пересечения:
7x -8 = x²
x²-7x+8 = 0
Мы вышли на квадратное уравнение, достаточно теперь найти его корни:
D = b² - 4ac = 49 - 32 = 17
x1 = (7 - √17) / 2; x2 = (7+√17) / 2
данные иксы, это абсциссы точек пересечения графиков.
По условию, нам надо найти сумму данных абсцисс. Значит,
x1 + x2 = (7-√17) / 2 + (7+√17)/2 = 14/2 = 7
7 - сумма абсцисс точек пересечения графиков. Задача выполнена.
Домножим обе части на 4
8sin²x - 12sinx + 1 = 0Данное уравнение является квадратным относительно sinх, сделаем замену: sinx = a, a ∈ [-1;1], тогда8а² - 12а + 1 = 0D = (-12)² - 4•8•1 = 144 - 32 = 112 a₁ = (12 - 4√7)/16 = (3 - √7)/4 ≈ 0,09sinx = (3-√7)/4x₁ = arcsin( (3-√7)/4 ) + 2πn, n ∈ Zx₂ = π - arcsin( (3-√7)/4 ) + 2πk, k ∈ Za₂ = (12 + 4√7)/16 = (3 + √7)/4 ≈ 1,41 ∉ [-1;1] ⇒ ∅ОТВЕТ: arcsin( (3-√7)/4 ) + 2πn ; π - arcsin( (3-√7)/4 ) + 2πk , n , k ∈ Z