Постройте график функции y= x^2 - 4x + 4 найти область значения функции
y= x² - 4x + 4 ;
y = (x -2)²
График этой функции парабола , получается из графики функции у =x² перемещением по положительному направлению оси абсцисс _Ox
( направо) на две единицы . Вершина параболы оказывается в точке
на оси абсцисс с координатой x =2 * * * точка B(0 ; 2)_точка миним. * * *
ветви направленные вверх (по "+ 0у" ) .
График ось ординат пересекает в точке (0 ; 4) * * *x =0 ⇒y =(0 -2)² =4.* * *
y=(x -2)² ≥0
Минимальное значение функции равно нулю : Minу =0 , если x =2 .
Максимальное значение не имеетю
Область значения функции : E(y) = [ 0 ; +∞)
1.В
Диагонали ромба не равны, они в точке пересечения делятся по полам.
2.
Зная что сумма внутренних углов четырехугольника 360° составим уровнение:
110+110+х+х=360
220+2х=360
2х=360-220
2х=140°
Х=70°
ответ:В
3.
S=a²
Увеличим в два раза:
S=(2a)²=4a²
ответ:Б, увеличится в 4 раза.
4.
Синус-отношение противолежайщего катета к гипотенузе.
По теореме Пифагора найдём гипотенузу:
5²+12²=25+144=169
√169=13
Синус равен-5/13
ответ:а
5.
Сначала найдём сумму внутренних углов в пятиугольнике:
180(n-2)=180(5-2)=180*3=540
Составим уровнение:
2х+4х+х+3х+8х=540
18х=540
Х=30
8*30=240°
ответ:В
6.
Найдем гипотенузу первого треугольника:
6²+8²=36+64=100
√100=10
Подобный ему треугольник в три раза больше него значит и катет будет в три раза больше:
6*3=18см
ответ:а
7.
Проведем две высоты и по теореме Пифагора найдём его:
10²-8²=100-64=36
√36=6
Найдем площадь трапеции:
S=Lh
L-средняя линия
h-высота
Найдем среднюю линию:
L=(4+20)÷2=24÷2=12
Подставляем:
S=12*6=72
ответ:72см²
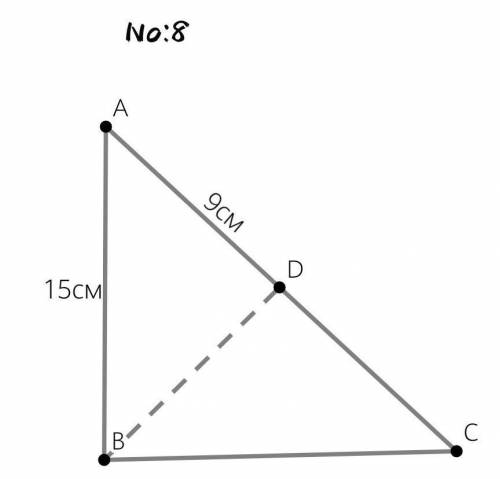
8.
15²=9*АС
225=9*АС
АС=25(гипотенуза)
По теореме Пифагора найдём катет:
25²-15²=625-225=400
√400=20
Найдем площадь:
S=1/2*15*20=150
ответ:150см²

Раскроем скобки.
8x+14x-12-21x=0
x=12