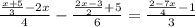
И так, сначала умножаем все выражение на 12 (т. к. 12 это НОК по отношению к 4, 6 и 3), получается, что:
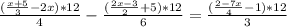
Сокращаем дроби и получаем:
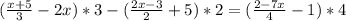
Отлично, мы значительно упростили изначальное выражение и теперь нам необходимо раскрыть скобки (умножить каждый член в скобках на множитель за ними), что мы и сделаем:
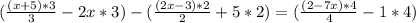
Как мы видим, получается очень красиво, т. к. все дроби просто-напросто сократятся:
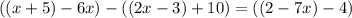
Снова раскроем скобки соблюдая все знаки (к знакам всегда стоит быть крайне внимательным при раскрытии скобок, так например в нашем случае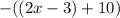 
раскроется как
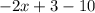т. к. минус на минус дает плюс, а минус на плюс дает минус):
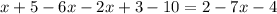
Супер, теперь уравнение приобрело совсем простой вид, проведем лишь косметические преобразования и сведем все подобные:
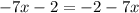
Переносим все неизвестные влево, а все, что известно вправо (не забываем при этом менять знаки):
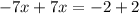
Считаем:
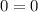
Видим, что наше уравнение является тождеством — а это значит, что его решением является любое значение x.
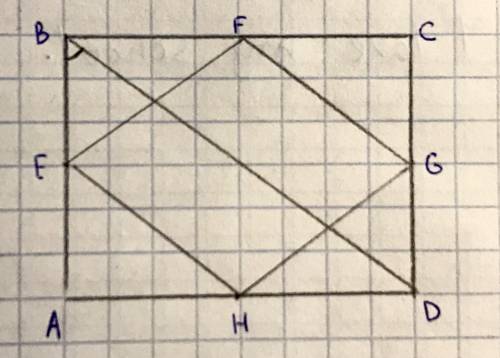
Найдём большую сторону прямоугольника. Она является катетом в прямоугольном ΔABD.
Для этого нам нужно сперва найти его гипотенузу. Сторона AB лежит против угла в 30° (∠BDA = 90° - ∠ABD = 90° - 60° = 30°).
Теорема: сторона, лежащая против угла в 30° в прямоугольном треугольнике, равняется половине гипотенузы.
BD = 2AB = 32 см .
По теореме Пифагора находим большую сторону прямоугольника:
BD² = AD² + AB²
32² = AD² + 16²
1024 = AD² + 256
AD² = 768
AD = √768 = √(256 * 3) = 16√3
Стороны BF, AH, HD и FC равны. Они равняются половинам сторон BC и AD, а, так как BC = AD, BC/2 = AD/2.
Соответственно, стороны EB, EA, CG и GD также равны.
Таким образом, прямоугольные ΔBEF, ΔCGF, ΔDGH и ΔAEH равны по двум катетам. Соответственно равны и их гипотенузы. Найдём их по той же теореме Пифагора:
EF² = BF² + BE²
EF² = (8√3)² + 8²
EF² = 192 + 64
EF² = 256
EF = 16
Периметр четырёхугольника равен 4EF = 64 см.
Четырёхугольник является ромбом, так как все его стороны равны.
