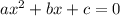
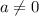, так как уравнение обращается в линейное.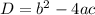
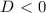уравнение не имеет решений (вообще имеет, но это в школе не проходят).
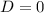то уравнение имеет 1 решение (корень).
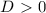- уравнение имеет 2 корня.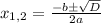
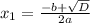
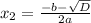
1+sinx·√(2ctgx) ≤ 0
Подкоренное выражение не может быть отрицательным
ctg x ≥ 0 0.5π ≥ x > 0 это в 1-й четверти
1.5π ≥ x > π это в 3-й четверти
в 1-й четверти sinx > 0 и выражение 1+sinx·√(2ctgx)> 0
в 3-й четверти sinx < 0 и выражение 1+sinx·√(2ctgx)может стать меньше 0, если
sinx·√(2ctgx) ≤ -1
делим на отрицательный синус
√(2ctgx) ≥ -1/sinx
обе части положительны
возводим в квадрат
2ctgx ≥ 1/sin²x
2ctgx ≥ 1 + ctg²x
1 + ctg²x - 2ctgx ≤ 0
(1 - ctgx)² ≤ 0
Квадрат любого числа не может быть отрицательным, поэтому остаётся только
равенство нулю:
1 - ctgx = 0
ctgx = 1 (четверть 3-я!)
х = 5/4π
Решение единственное: при х = 5/4π выражение 1+sinx·√(2ctgx) = 0
ну, и, разумеется следует добавить 2πn, тогда решение такое:
х = 5/4π +2πn
6³=216