«Над пропастью во ржи», также в других переводах — «Ловец на хлебном поле», «Обрыв на краю ржаного поля детства» (англ. The Catcher in the Rye — «Ловец во ржи», 1951) — роман американского писателя Джерома Сэлинджера, входит в 100 мировых книг. В ней от лица 16-летнего юноши, по имени Холден откровенно рассказывается о его обострённом восприятии американской действительности и неприятии общих канонов и морали современного общества. Произведение имело огромную популярность как среди молодёжи, так и среди взрослого населения, оказав существенное влияние на мировую культуру второй половины XX века.
Роман был переведён почти на все основные языки мира[1]. В 2005 году журнал Time включил роман в список 100 лучших англоязычных романов, написанных начиная с 1923 года, а издательство Modern Library[en] включило его в список 100 лучших англоязычных романов XX столетия. Однако, несмотря на это в США роман часто подвергался критике и запрещён в нескольких школах из-за большого количества нецензурной лексики
Объяснение:
По определению, 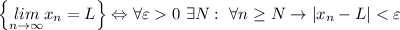
Т.к. в обоих случаях нужно обосновать, что L=0, определение преобразуется в утверждение 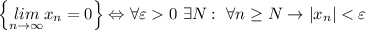
2) 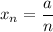
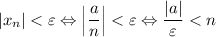
А значит, если взять ![N=\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/0d89e.png) (*),
(*),  . И правда:
. И правда: 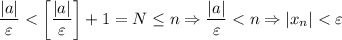
(*) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{|a|}{\varepsilon}\right] +1](/tpl/images/3820/0626/ae843.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (*)
А это и означает, что предел данной последовательности равен 0
4) 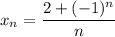

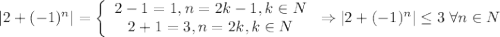
А значит, если взять ![N=\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/a4ca4.png) (**),
(**),  . И правда:
. И правда: ![\dfrac{|2+(-1)^n|}{\varepsilon}\leq\dfrac{3}{\varepsilon}< \left[\dfrac{3}{\varepsilon}\right] +1=N\leq n \Rightarrow \dfrac{|2+(-1)^n|}{\varepsilon}< n \Rightarrow |x_n|](/tpl/images/3820/0626/49458.png)
(**) Очевидно, что для любого допустимого значения  выражение
выражение ![\left[\dfrac{3}{\varepsilon}\right] +1](/tpl/images/3820/0626/698f8.png) определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
определено и конечно, и при этом натуральное число (как сумма неотрицательного целого числа и 1). (**)
А это и означает, что предел данной последовательности равен 0
___________________________
2) a=1. Тогда 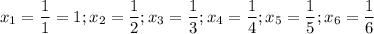
4)

___________________________
Обозначения и некоторые св-ва: {x} - дробная часть числа x, [x] - целая часть числа x. 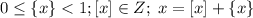

Дискриминант уравнения D = b² - 4ac;
A) a = 1; b = 3; c = -10; D = 9+40 = 49; D>0, 2 корня.
Б) a = 1; b = -3; c = 3; D = 9 - 12 = -3; D<0, корней нет.
В) a =4; b = 4; c = 1; D = 16-16 = 0 D = 0, 1 корень